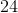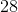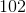Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : 3-Dimensional Geometry

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Advanced Geometry

The circumference of the base of a cone is 100; the height of the cone is equal to the diameter of the base. Give the surface area of the cone (nearest whole number).

Possible Answers:

2,575

2,385

1,589

1,779

8,443

Correct answer:

2,575

Explanation:

The formula for the surface area of a cone with base of radius and slant height is

$A = \pi r^{2} + \pi r l$ .

The diameter of the base is the circumference divided by $\pi$ , which is

$d = C \div (2\pi ) \approx 100 \div 3.14 \approx 31.83$

This is also the height .

The radius is half this, or

$r = d \div 2 \approx 31.83 \div 2 \approx 15.92$

The slant height can be found by way of the Pythagorean Theorem:

$l = \sqrt{r^{2}+ h ^{2}}$

$l \approx \sqrt{15.92^{2}+ 31.83 ^{2}}$

$l \approx \sqrt{253.30+ 1,013.21}$

$l \approx \sqrt{1266.51}$

$l \approx 35.60$

Substitute in the surface area formula:

$A = \pi r^{2} + \pi r l$

$A \approx 3.14 \cdot 15.92 ^{2} + 3.14 \cdot 15.92 \cdot 35.60$

$A \approx 795.8+ 1,780.1$

$A \approx 2,575$

Report an Error

Example Question #51 : 3 Dimensional Geometry

If a cone were unfurled into a 2-dimensional figure. The lateral area of the cone would look most like which figure?

Possible Answers:

Triangle

Circle

Sector of a Circle

Rectangle

Correct answer:

Sector of a Circle

Explanation:

When creating a net image of a 3D figure - one imagines it is made of paper and is unfurled into its' 2D form. The lateral portion of the cone cone would be unfurled into the image of a Sector of a Circle. To include the full surface area of the cone a circle is included to form the base of the cone as in the figure below. The lateral area portion is the top part of the figure below.

Cone net

Report an Error

Example Question #52 : 3 Dimensional Geometry

Find the surface area of a cube with side length of 6in.

Possible Answers:

24cm^2

18cm^2

250cm^2

216cm^2

36cm^2

Correct answer:

216cm^2

Explanation:

A cube is made up of 6 identical sides. Find the area of one side and multiplying it by 6 will result in the surface area of a cube.

S=6a^2

a is the side length, in this case 6in.

S=6(6cm)^2=6*36cm^2=216cm^2

Report an Error

Example Question #27 : Surface Area

What is the surface area of a cylinder with height 10 and radius 7?

Possible Answers:

$238\pi$

$163\pi$

$140\pi$

$300\pi$

$98\pi$

Correct answer:

$238\pi$

Explanation:

The formula of the surface area of a cylinder is:

$SA=2\pi rh+2\pi r^2$

In this problem h is 10 and r is 7. Substituting in those values gives us:

$SA=2\pi 7*10+2\pi 7^2$

Simplifying and combining the like terms results in:

$SA=140\pi+98\pi=238\pi$

Report an Error

Example Question #22 : Surface Area

Figure not drawn to scale.

Box example

Find the surface area of the box above.

Possible Answers:

Surface area: 82 yd²

Surface area: 84 yd²

Surface area: 82 yd³

Surface area: 84 yd³

Surface area: 48 yd²

Correct answer:

Surface area: 82 yd²

Explanation:

Box example

You can find the surface area of a box by following the equation below:

$\small \small \small Surface Area = 2(length\times height) + 2(length\times depth) + 2(height\times depth)$

$\small \small \small 2(7\times 3) + 2(7\times 2) + 2(3\times 2)=$

$\small 2(21) + 2(14) + 2(6)=$

$\small \small 42 + 28 + 12= 82$

The surface area of the box is 82yd²(remember that area measurements are square units NOT cubic units)

Report an Error

Example Question #29 : Surface Area

Box 3

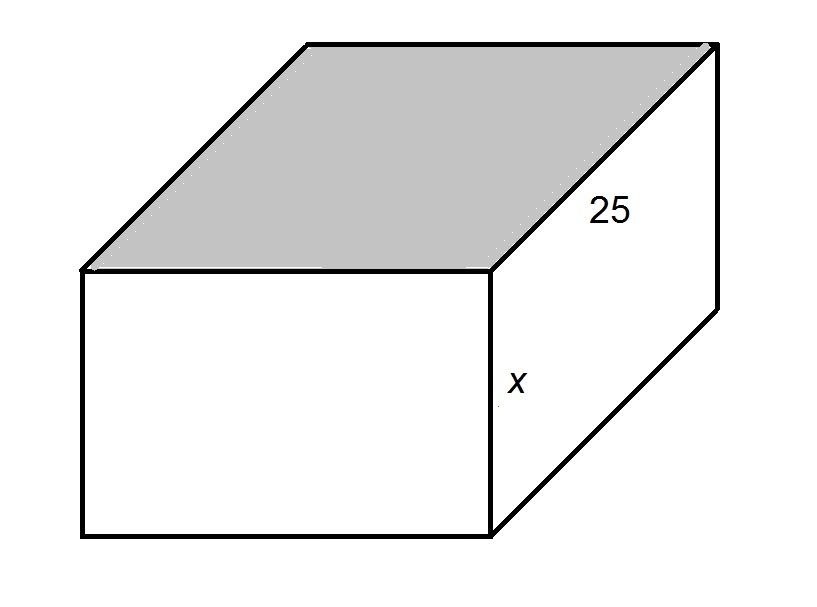
The shaded face of the provided rectangular prism is a square. If the surface area of the prism is , give in terms of .

Possible Answers:

$x = \frac{-25+\sqrt{4A+625}}{4}$

$x = \frac{A}{625}$

$x=\frac{ A - 1,250}{100}$

$x = \frac{-50+\sqrt{2A+2,500}}{2}$

$x=\frac{ A -2,500}{50}$

Correct answer:

$x=\frac{ A - 1,250}{100}$

Explanation:

Since the top face of the prism is a square, the common sidelength - and the missing dimension - is 25.

The surface area 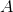of a rectangular prism with length , width , and height can be found using the formula

2LW + 2 WH + 2LH = A .

Setting H= x, L=W= 25 , and solving for :

$2 \cdot 25 \cdot 25 + 2 \cdot 25 \cdot x + 2 \cdot 25 \cdot x = A$

1,250 + 50x + 50 x = A

100 x + 1,250 = A

100 x + 1,250 - 1,250 = A - 1,250

100 x = A - 1,250

$\frac{100 x }{100}=\frac{ A - 1,250}{100}$

$x=\frac{ A - 1,250}{100}$

Report an Error

Example Question #1 : Faces, Face Area, And Vertices

How many vertices does a polyhedron with twenty faces and thirty edges have?

Possible Answers:

Correct answer:

Explanation:

By Euler's Formula, the relationship between the number of vertices , the number of faces , and the number of edges of a polyhedron is

V + F - E = 2

Set F = 20 and E = 30 , and solve for :

V + 20 - 30 = 2

V -10 = 2

V = 12

The polyhedron has tweve vertices.

Report an Error

Example Question #1 : Faces, Face Area, And Vertices

How many edges does a polyhedron with nine vertices and eleven faces have?

Possible Answers:

Correct answer:

Explanation:

By Euler's Formula, the relationship between the number of vertices , the number of faces , and the number of edges of a polyhedron is

V + F - E = 2

Set V= 9 and F = 11 and solve for :

9 +11 - E = 2

20 - E = 2

E = 18

The polyhedron has eighteen edges.

Report an Error

Example Question #53 : 3 Dimensional Geometry

A rectangular prism has a height of 4 in., length of 8in., and a width of 7in. Find the volume of the prism.

Possible Answers:

$230\ \textup{in.}$

$17\ \textup{in.}$

$146\ \textup{in.}$

$224\ \textup{in.}$

Correct answer:

$224\ \textup{in.}$

Explanation:

To find the volume of a rectangular prism we use the equation of:

V=l*w*h

Now substituting in our values we get:

V=8*7*4

V=56*4

V=224

Report an Error

Example Question #2 : Other 3 Dimensional Geometry

What is the volume of a triangular prism having a base of 2, a height of 8, and second height of 14?

Possible Answers:

102

112

Correct answer:

112

Explanation:

To find the volume of a triangular prism we use the equation

$V= \frac{1}{2}(b*h)*h_2$

In our case our b=2, h=8, h_2=14

Therefore,

$V=\frac{1}{2}(2*8)*14$

$V=\frac{1}{2}(16)*14$

V=8*14

V=112

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Chisom
Certified Tutor

Georgia Southern University, Bachelor of Science, Biochemistry. University of Georgia, Current Grad Student, Pharmacy.

View SAT Subject Test in Mathematics Level 1 Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View SAT Subject Test in Mathematics Level 1 Tutors

Austyn
Certified Tutor

Morehead State University, Bachelor of Education, Mathematics Teacher Education. Morehead State University, Master of Arts, M...

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Seattle, MCAT Tutors in Phoenix, Reading Tutors in Phoenix, Statistics Tutors in Los Angeles, Computer Science Tutors in Phoenix, Math Tutors in Phoenix, Biology Tutors in Los Angeles, SAT Tutors in Atlanta, SSAT Tutors in Chicago, Computer Science Tutors in New York City

Popular Courses & Classes

LSAT Courses & Classes in San Diego, SSAT Courses & Classes in Miami, GRE Courses & Classes in Los Angeles, MCAT Courses & Classes in Miami, GRE Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Chicago, GRE Courses & Classes in San Diego, GRE Courses & Classes in Atlanta, GRE Courses & Classes in Chicago, MCAT Courses & Classes in San Diego

Popular Test Prep

SSAT Test Prep in Atlanta, ISEE Test Prep in Boston, LSAT Test Prep in Washington DC, LSAT Test Prep in New York City, ISEE Test Prep in San Diego, ACT Test Prep in Philadelphia, GMAT Test Prep in Los Angeles, SAT Test Prep in Seattle, MCAT Test Prep in Philadelphia, ACT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : 3-Dimensional Geometry

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #21 : Advanced Geometry

Example Question #51 : 3 Dimensional Geometry

Example Question #52 : 3 Dimensional Geometry

Example Question #27 : Surface Area

Example Question #22 : Surface Area

The surface area of the box is 82yd²(remember that area measurements are square units NOT cubic units)

Example Question #29 : Surface Area

Example Question #1 : Faces, Face Area, And Vertices

Example Question #1 : Faces, Face Area, And Vertices

Example Question #53 : 3 Dimensional Geometry

Example Question #2 : Other 3 Dimensional Geometry

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback:

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : 3-Dimensional Geometry

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #21 : Advanced Geometry

Example Question #51 : 3 Dimensional Geometry

Example Question #52 : 3 Dimensional Geometry

Example Question #27 : Surface Area

Example Question #22 : Surface Area

The surface area of the box is 82yd2 (remember that area measurements are square units NOT cubic units)

Example Question #29 : Surface Area

Example Question #1 : Faces, Face Area, And Vertices

Example Question #1 : Faces, Face Area, And Vertices

Example Question #53 : 3 Dimensional Geometry

Example Question #2 : Other 3 Dimensional Geometry

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

The surface area of the box is 82yd²(remember that area measurements are square units NOT cubic units)