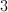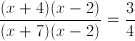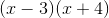All PSAT Math Resources
Example Questions
Example Question #1 : Binomials
Which of these expressions can be simplified further by collecting like terms?
None of the expressions in the other choices can be simplified further
None of the expressions in the other choices can be simplified further
A binomial can be simplified further if and only if the two terms have the same combination of variables and the same exponents for each like variable. This is not the case in any of the four binomials given, so none of the expressions can be simplified further.
Example Question #21 : Polynomials
Solve for 
Factor the expression
numerator: find two numbers that add to 2 and multiply to -8 [use 4,-2]
denominator: find two numbers that add to 5 and multiply to -14 [use 7,-2]
new expression:
Cancel the 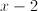
Example Question #3 : Binomials
Give the coefficient of 
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add:
The correct response is 
Example Question #2 : Binomials
Give the coefficient of 

If the expression 

or, equivalently, the coefficient of 
Therefore, the 

Example Question #3 : Binomials
Give the coefficient of 

If the expression 

or, equivalently, the coefficient of 
Therefore, the 

Example Question #1 : How To Find The Value Of The Coefficient
Give the coefficient of 

If the expression 

or, equivalently, the coefficient of 
Therefore, the 
Example Question #1 : Coefficients
Give the coefficient of 

While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add:
The correct response is -122.
Example Question #1 : How To Find The Value Of The Coefficient
Give the coefficient of 

While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add: 
The correct response is 
Example Question #41 : Algebra
Multiply the binomial.
By multiplying with the foil method, we multiply our first values giving 


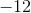
Example Question #41 : Algebra
Factor the following expression completely:
We must begin by factoring out 
Next, we must find two numbers that sum to 

Thus, our final answer is:
Certified Tutor
All PSAT Math Resources