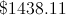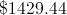All PSAT Math Resources
Example Questions
Example Question #3 : How To Find Simple Interest
Ted works over the summer and makes $9 per hour. He works for 20 hours each week for 10 weeks. After paying 10% in taxes, he buys a bike for $500 and puts the rest of his money in the bank.
If Ted's bank pays 5% interest on the total sum once per year, and Ted doesn't add or remove anything from the account, how much money (rounded to the nearest cent) will Ted have in 5 years?
To start, we see that Ted works for 20 hours per week for 10 weeks. This means he works a total of 200 hours over the summer. He is paid $9 dollars each hour. Therefore he makes $9 x 200 hours = $1800 total over the summer. He then has to pay 10% in taxes, or .1 x $1800, leaving him with 
Now we have to find out how much he will have 5 years later. Since the bank pays 5% interest each year, we know that he will make 5% of what he has each year. He starts with $1,120. 5% of this value is 
This is also the same as multiplying instead by 1.05. We repeat this step 5 times, giving us:
Example Question #4 : How To Find Simple Interest
Jane borrows 


Use the simple interest formula:
Interest equals the initial amount multiplied by the annual interest rate multiplied by the number of years:
Let 
Let 
Let 
Let 
Therefore:
Example Question #1 : How To Find The Percent Of Decrease
At a certain store, prices for all items were assigned in January. Each month after that, the price was 20% less than the price the previous month. If the price of an item was x dollars in January, approximately what was the price in dollars of the item in June?
0.51x
0.66x
0.33x
0.81x
0.12x
0.33x
The question tells us that the price in January was x. To find the price in February, we decrease the price of x by 20%, which is the same as taking 80% of x. (In general, a P% decrease of a number is the same as (100 – P)% times that number). Continue to take 0.8 times the previous month's price to find the next month's price until we have the price for June, as follows:
January Price: x
February Price: 0.8 * January Price = 0.8x
March Price: 0.8 * February Price = 0.8 * 0.8x = 0.82 * x
April Price: 0.8 * March Price = 0.8 * 0.8 * 0.8x = 0.83 * x
May Price: 0.8 * April Price = 0.8 * 0.8 * 0.8 * 0.8x = 0.84 * x
June Price: 0.8 * May Price = 0.8 * 0.8 * 0.8 * 0.8 * 0.8x = 0.85 * x; therefore, the price in June was 0.85 ≈ 0.328 ≈ 0.33 times the original price.
Example Question #2 : How To Find The Percent Of Decrease
The sale of a tablet decreased from $500 to $450. By what percentage did the cost decrease?
20%
10%
15%
5%
1%
10%
Set up the following ratio
50/500 = n/100
The cost of the tablet decreased by $50. The original cost is $500; therefore, 50 is the numerator and 500 is the denominator on the left side of the ratio.
Since a percentage is a part of a whole, n symbolizes the the percentage decrease.
To solve for n, you can cross multiply. So, 50(100) = n(500).
n = 10%
Example Question #1 : How To Find The Percent Of Decrease
On Monday, the price of a shirt costs x dollars. On Tuesday, the manager puts the shirt on sale for 10% off Monday's price. On Wednesday, the manager increases the price of the shirt by 10% of Tuesday's price. Describe the change in price from Monday to Wednesday.
10% decrease
10% increase
1% increase
1% decrease
No change
1% decrease
To find the cost on Tuesday, take 10% off Monday's price. In other words, find 90% of Monday's price. This is simply 0.9x. If we are to now add 10% of this value back onto itself to find Wednesday's price, we want 100% + 10%, or 110% of 0.9x.
1.1(0.9x) = 0.99x
This value is 1% smaller than x.
Example Question #251 : Arithmetic
If the length of a rectangle is increased by thirty percent, which of the following most closely approximates the percent by which the rectangle's width must decrease, so that the area of the rectangle remains unchanged?
21
25
30
17
23
23
Example Question #1 : How To Find The Percent Of Decrease
If the price of a TV was decreased from $3,000 to $1,800, by what percent was the price decreased?
60%
20%
50%
40%
30%
40%
The price was lowered by $1,200 which is 40% of $3,000.
Example Question #1 : How To Find The Percent Of Decrease
If a rectangle's length decreases by fifteen percent, and its width decreases by twenty percent, then by what percent does the rectangle's area decrease?
32
45
40
36
35
32
Let's call the original length and width of the rectangle 

The initial area, 
Next, let 


We are asked to find the change in the area, which essentially means we want to compare 








First, we are told that the length is decreased by fifteen percent. We can think of the full length as 100% of the length. If we take away fifteen percent, we are left with 100 – 15, or 85% of the length. In other words, the final length is 85% of the original length. We can represent 85% as a decimal by moving the decimal two places to the left.


Similarly, if we decrease the width by 20%, we are only left with 80% of the width.


We can now express the final area in terms of 




Lastly, let's apply the formula for percent of change, which will equal the change in the area divided by the original area. The change in the area is equal to the final area minus the original area.
percent change = 
=
=
The negative sign indicates that the rectangle's area decreased. The change in the area was a decrease of 32%.
The answer is 32.
Example Question #91 : Percentage
The cost of a load of laundry is reduced by 

The original reduction brings the total to 



Example Question #3 : How To Find The Percent Of Decrease
The cost of a shirt in January is 
We must know the original cost to find the answer
The best way to answer this question is to plug in a number for n. Since you are working with percentages, it may be easiest to use 100 for n.
We know that in the month of February, the cost of this shirt was decreased by 10%. Because 10% of 100 is $10, the new cost of the shirt is $90.
In March, the cost of the shirt decreased another 10%. 10% of 90 is 9, so the cost of the shirt is now $81.
To find the total percentage decrease, you must divide 81 by 100 and subtract it from 1.
1 – (81/100) = 1 – 0.81 = 0.19
The total decrease was 19%.
All PSAT Math Resources