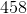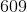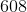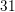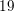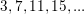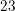All PSAT Math Resources
Example Questions
Example Question #22 : Sequences
In a certain sequence, an+1 = (an)2 – 1, where an represents the nth term in the sequence. If the third term is equal to the square of the first term, and all of the terms are positive, then what is the value of (a2)(a3)(a4)?
63
6
72
24
48
48
Let a1 be the first term in the sequence. We can use the fact that an+1 = (an)2 – 1 in order to find expressions for the second and third terms of the sequence in terms of a1.
a2 = (a1)2 – 1
a3 = (a2)2 – 1 = ((a1)2 – 1)2 – 1
We can use the fact that, in general, (a – b)2 = a2 – 2ab + b2 in order to simplify the expression for a3.
a3 = ((a1)2 – 1)2 – 1
= (a1)4 – 2(a1)2 + 1 – 1 = (a1)4 – 2(a1)2
We are told that the third term is equal to the square of the first term.
a3 = (a1)2
We can substitute (a1)4 – 2(a1)2 for a3.
(a1)4 – 2(a1)2 = (a1)2
Subtract (a1)2 from both sides.
(a1)4 – 3(a1)2 = 0
Factor out (a1)2 from both terms.
(a1)2 ((a1)2 – 3) = 0
This means that either (a1)2 = 0, or (a1)2 – 3 = 0.
If (a1)2 = 0, then a1 must be 0. However, we are told that all the terms of the sequence are positive. Therefore, the first term can't be 0.
Next, let's solve (a1)2 – 3 = 0.
Add 3 to both sides.
(a1)2 = 3
Take the square root of both sides.
a1 = ±√3
However, since all the terms are positive, the only possible value for a1 is √3.
Now, that we know that a1 = √3, we can find a2, a3, and a4.
a2 = (a1)2 – 1 = (√3)2 – 1 = 3 – 1 = 2
a3 = (a2)2 – 1 = 22 – 1 = 4 – 1 = 3
a4 = (a3)2 – 1 = 32 – 1 = 9 – 1 = 8
The question ultimately asks for the product of the a2, a3, and a4, which would be equal to 2(3)(8), or 48.
The answer is 48.
Example Question #23 : Sequences
In the given sequence, the first term is 3 and each term after is one less than three times the previous term.
What is the sixth term in the sequence?
The fourth term is: 3(23) – 1 = 69 – 1 = 68.
The fifth term is: 3(68) – 1 = 204 – 1 = 203.
The sixth term is: 3(203) – 1 = 609 – 1 = 608.
Example Question #31 : Sequences
Consider the following sequence of numbers:
What will be the 8th term in the sequence?
56
51
60
49
58
51
Each number in the sequence in 7 more than the number preceding it.
The equation for the terms in an arithmetic sequence is an = a1 + d(n-1), where d is the difference.
The formula for the terms in this sequence is therefore an = 2 + 7(n-1).
Plug in 8 for n to find the 8th term:
a8 = 2 + 7(8-1) = 51
Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence
The second and fourth terms of an arithmetic sequence are 9 and 18, respectively. What is its first term?
The difference between the second and fourth terms of an arithmetic sequence is twice the common difference - or, equivalently, the common difference is half the difference between the second and fourth terms.
The common difference can be subtracted from the second term to obtain the first term:
Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence
A sequence of numbers is represented by the equation 



Take the equation that represents the 

The value of the 9th term is 747.
Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence
You are given a sequence with the same difference between consecutive terms. We know it starts at 

From the given information, we know 
Example Question #1 : How To Find The Next Term In An Arithmetic Sequence
Each term in the sequence is one less than twice the previous term.
So, 
Example Question #12 : Nth Term Of An Arithmetic Sequence
What is the next number in the following series: 0, 3, 8, 15, 24 . . . ?
40
35
32
37
41
35
The series is defined by n2 – 1 starting at n = 1. The sixth number in the series then equal to 62 – 1 = 35.
Example Question #2 : How To Find The Next Term In An Arithmetic Sequence
A sequence of numbers is as follows:
What is the sum of the first seven numbers in the sequence?
490
719
248
1529
621
621
The pattern of the sequence is (x+1) * 2.
We have the first 5 terms, so we need terms 6 and 7:
(78+1) * 2 = 158
(158+1) * 2 = 318
3 + 8 + 18 +38 + 78 + 158 + 318 = 621
Example Question #1 : How To Find The Next Term In An Arithmetic Sequence
Find the 
Notice that in the sequence
each term increases by 
It is always good strategy when attempting to find a pattern in a sequence to examine the difference between each term.
We continue the pattern to find:
The 
The 
The 
It is useful to note that the sequence is defined by,
where n is the number of any one term.
We can solve
to find the 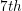
Certified Tutor
All PSAT Math Resources