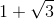Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Other Polygons

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Other Polygons

Heptagon

Note: Figure NOT drawn to scale.

The perimeter of the above polygon is 225. Also, B = A + C .

Evaluate .

Possible Answers:

$B = 37 \frac{1}{2}$

$B = 56\frac{1}{4}$

$B = 34\frac{1}{6}$

Insufficient information exists to answer the question.

$B = 51\frac{1}{4}$

Correct answer:

$B = 51\frac{1}{4}$

Explanation:

To get the expression equivalent to the perimeter, add the lengths of the sides:

P = A + A + B + B + C + C + 20

Since the perimeter is 225, we can simplify this to

225= 2A + 2B + 2C + 20

and, furthermore, since B = A + C ,

2A + 2B + 2C = 205

2B +2A + 2C = 205

$2B +2\left (A + C \right )= 205$

2B +2B= 205

4B = 205

$B = 51\frac{1}{4}$

Report an Error

Example Question #421 : Geometry

Regular Octagon ABCDEFGH has sidelength 1.

Give the length of diagonal $\overline{AD}$ .

Possible Answers:

$\frac{2 + \sqrt{3}}{2}$

$1 + \sqrt{3}$

$\frac{2 + \sqrt{2}}{2}$

$1 + \sqrt{2}$

Correct answer:

$1 + \sqrt{2}$

Explanation:

The trick is to construct segments perpendicular to $\overline{AD}$ from and , calling the points of intersection and respectively.

Octagon_1

Each interior angle of a regular octagon measures

$\frac{\left ( 8 - 2\right ) 180^{\circ }}{8} = 135^{\circ }$ ,

and by symmetry, $m \angle HAD = m \angle ADE = 90^{\circ }$ ,

so $m \angle BAX = m \angle CDY= 45^{\circ }$ .

This makes $\Delta BAX$ and $\Delta CDY$ $45^{\circ } -45^{\circ } -90^{\circ }$ triangles.

Since their hypotenuses are sides of the octagon with length 1, then their legs - in particular, $\overline{AX}$ and $\overline{YD}$ - have length $\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$ .

Also, since a rectangle was formed when the perpendiculars were drawn, XY = BC = 1 .

The length of diagonal $\overline{AD}$ is

$AD = AX + XY + YD = \frac{\sqrt{2}}{2}+ 1 + \frac{\sqrt{2}}{2} = 1 + \sqrt{2}$ .

Report an Error

Example Question #1 : How To Find The Length Of A Diagonal Of A Polygon

Regular Polygon ABCDEFGHIJKL (a twelve-sided polygon, or dodecagon) has sidelength 1.

Give the length of diagonal $\overline{AD}$ to the nearest tenth.

Possible Answers:

$\frac{2 + \sqrt{2}}{2}$

$1 + \sqrt{2}$

$\frac{2 + \sqrt{3}}{2}$

$1 + \sqrt{3}$

Correct answer:

$1 + \sqrt{3}$

Explanation:

The trick is to construct segments perpendicular to $\overline{AD}$ from and , calling the points of intersection and respectively.

Dodecagon

Each interior angle of a regular dodecagon measures

$\frac{\left ( 12 - 2\right ) 180^{\circ }}{12} = 150^{\circ }$ .

Since $\overline{BX}$ and $\overline{CY}$ are perpendicular to $\overline{AD}$ , it can be shown via symmetry that they are also perpendicular to $\overline{BC}$ . Therefore,

$\angle ABX$ and $\angle DCY$ both measure $60^{\circ }$

and $\Delta ABX$ and $\Delta DCY$ are $30^{\circ}-60^{\circ}-90^{\circ}$ triangles with long legs $\overline{AX}$ and $\overline{YD}$ . Since their hypotenuses are sides of the dodecagon and therefore have length 1,

$AX = YD = \frac{\sqrt{3}}{2}$ .

Also, since Quadrilateral BCXY is a rectangle, XY = BC = 1 .

The length of diagonal $\overline{AD}$ is $AD = AX + XY + YD = \frac{\sqrt{3}}{2}+ 1 + \frac{\sqrt{3}}{2} = 1 + \sqrt{3}$ .

Report an Error

Example Question #1 : How To Find The Perimeter Of A Polygon

Rectangle_3

Note: Figure NOT drawn to scale.

Refer to the above figure. The white trapezoid is isosceles. Give the perimeter of the blue polygon.

Possible Answers:

318

$264 + 18 \sqrt{3}$

$264 + 18 \sqrt{2}$

$264 + 36 \sqrt{2}$

336

Correct answer:

$264 + 36 \sqrt{2}$

Explanation:

The lower base of this trapezoid is 100 - 64 = 36 units longer than the upper base, and being isosceles, it is symmetrical. As a result, the lower leg of the right triangle at bottom is half this difference, or 18, which is the same as the upper leg. That makes the right triangle isosceles, and, therefore, a 45-45-90 triangle. 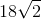Subsequently, the hypotenuse, which is one leg of the trapezoid, has length $\sqrt{2}$ times a leg of the triangle, or $18 \sqrt{2}$ .

The blue polygon has two sides that are the legs of this isosceles trapezoid, both of which have length $18 \sqrt{2}$ ; its other three sides are of length 64, 50, 100, and 50. Add them:

$P = 100 + 64 + 50 + 50 + 18 \sqrt{2}+ 18 \sqrt{2} = 264 + 36 \sqrt{2}$

Report an Error

View PSAT Mathematics Tutors

Danielle
Certified Tutor

View PSAT Mathematics Tutors

Kavya
Certified Tutor

University of Kansas, Bachelor of Science, Cellular and Molecular Biology.

View PSAT Mathematics Tutors

Darian
Certified Tutor

University of North Texas, Current Undergrad Student, English.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Dallas Fort Worth, SSAT Tutors in Atlanta, GRE Tutors in Atlanta, ACT Tutors in Atlanta, Reading Tutors in Chicago, SSAT Tutors in San Diego, Statistics Tutors in Atlanta, Biology Tutors in Seattle, Statistics Tutors in Denver, LSAT Tutors in Los Angeles

Popular Courses & Classes

GMAT Courses & Classes in Atlanta, GRE Courses & Classes in Atlanta, MCAT Courses & Classes in Atlanta, SAT Courses & Classes in Washington DC, Spanish Courses & Classes in Los Angeles, MCAT Courses & Classes in Houston, MCAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Houston, LSAT Courses & Classes in Washington DC, SAT Courses & Classes in San Diego

Popular Test Prep

GMAT Test Prep in Houston, MCAT Test Prep in Los Angeles, SAT Test Prep in Washington DC, GMAT Test Prep in Chicago, SSAT Test Prep in Philadelphia, GRE Test Prep in Washington DC, ISEE Test Prep in New York City, GRE Test Prep in Miami, GMAT Test Prep in San Diego, MCAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Other Polygons

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #21 : Other Polygons

Example Question #421 : Geometry

Example Question #1 : How To Find The Length Of A Diagonal Of A Polygon

Example Question #1 : How To Find The Perimeter Of A Polygon

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: