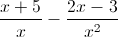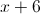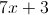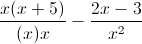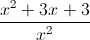All PSAT Math Resources
Example Questions
Example Question #1 : How To Subtract Rational Expressions With Different Denominators
Simplify.
Possible Answers:
Correct answer:
Explanation:
Determine an LCD (Least Common Denominator) between 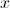
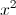
LCD =
Multiply the top and bottom of the first rational expression by 

Distribute the 

Now you can subtract because both rational expressions have the same denominators.
Final Answer.
Alisha
Certified Tutor
Certified Tutor
University of Wisconsin-Madison, Bachelor in Arts, Mathematics. University of South Florida-Main Campus, Master of Arts, Prem...
All PSAT Math Resources
Popular Subjects
Chemistry Tutors in Denver, ACT Tutors in Chicago, GRE Tutors in Boston, Biology Tutors in Miami, Math Tutors in Los Angeles, SSAT Tutors in Chicago, Biology Tutors in New York City, Reading Tutors in Los Angeles, Reading Tutors in Chicago, ACT Tutors in Houston
Popular Courses & Classes
GMAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Philadelphia, ACT Courses & Classes in New York City, GMAT Courses & Classes in San Diego, SAT Courses & Classes in Denver, SSAT Courses & Classes in Washington DC, GMAT Courses & Classes in Atlanta, Spanish Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Denver, LSAT Courses & Classes in Chicago
Popular Test Prep
MCAT Test Prep in Houston, GMAT Test Prep in Denver, SSAT Test Prep in San Diego, GRE Test Prep in San Francisco-Bay Area, LSAT Test Prep in Denver, ISEE Test Prep in Denver, ACT Test Prep in Dallas Fort Worth, GMAT Test Prep in Dallas Fort Worth, GMAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Atlanta