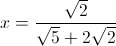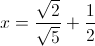Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : How to find the common factors of squares

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Factoring And Simplifying Square Roots

Solve for $\dpi{100} x$ :

$x\sqrt{45}+x\sqrt{72}=\sqrt{18}$

Possible Answers:

$x=\frac{\sqrt{5}}{\sqrt{2}}+2$

$x=3$

$x=\sqrt{9}$

$x=\frac{\sqrt{2}}{\sqrt{5}}+\frac{1}{2}$

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

Correct answer:

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

Explanation:

$x\sqrt{45}+x\sqrt{72}=\sqrt{18}$

Notice how all of the quantities in square roots are divisible by 9

$x\sqrt{9\times 5}+x\sqrt{9\times 8}=\sqrt{9\times 2}$

$x\sqrt{9}\sqrt{5}+x\sqrt{9}\sqrt{4\times 2}=\sqrt{9}\sqrt{2}$

$3x\sqrt{5}+3x\sqrt{4}\sqrt{2}=3\sqrt{2}$

$3x\sqrt{5}+6x\sqrt{2}=3\sqrt{2}$

$x(3\sqrt{5}+6\sqrt{2})=3\sqrt{2}$

$x=\frac{3\sqrt{2}}{3\sqrt{5}+6\sqrt{2}}$

Simplifying, this becomes

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

Report an Error

Example Question #51 : Simplifying Square Roots

If m and n are postive integers and 4^m = 2ⁿ, what is the value of m/n?

Possible Answers:

1/2

Correct answer:

1/2

Explanation:

2²= 4. Also, following the rules of exponents, 4¹= 1.
One can therefore say that m = 1 and n = 2.
The question asks to solve for m/n. Since m = 1 and n = 2, m/n = 1/2.

Report an Error

Example Question #21 : Basic Squaring / Square Roots

Simplify the radical:

$\sqrt{320}$

Possible Answers:

$8\sqrt{20}$

$8\sqrt{5}$

$4\sqrt{5}$

$4\sqrt{20}$

$\sqrt{320}$

Correct answer:

$8\sqrt{5}$

Explanation:

$\sqrt{320}=\sqrt{2\times 160}=\sqrt{2\times 2\times 80}=2\sqrt{80}=2\sqrt{2\times 40}=2\sqrt{2\times 2\times 20}=2\times 2\times \sqrt{20}=4\sqrt{2\times 10}=4\sqrt{2\times 2\times 5}=4\times 2\times \sqrt{5}=8\sqrt{5}$

Report an Error

View PSAT Mathematics Tutors

Ulises
Certified Tutor

Arizona State University, Bachelor in Arts, History.

View PSAT Mathematics Tutors

Shakeel
Certified Tutor

View PSAT Mathematics Tutors

Maziar
Certified Tutor

Tehran Polytechnic, Mechanical Engineer, Mechanical Engineering. New Mexico State University-Main Campus, Doctor of Philosoph...

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Chicago, LSAT Tutors in Philadelphia, Computer Science Tutors in Denver, Computer Science Tutors in San Diego, SSAT Tutors in Chicago, GRE Tutors in Atlanta, Calculus Tutors in Phoenix, ISEE Tutors in Washington DC, SSAT Tutors in Seattle, GMAT Tutors in Chicago

Popular Courses & Classes

LSAT Courses & Classes in New York City, ACT Courses & Classes in Seattle, SSAT Courses & Classes in Denver, ISEE Courses & Classes in Houston, SAT Courses & Classes in San Diego, GMAT Courses & Classes in Washington DC, SAT Courses & Classes in Denver, SSAT Courses & Classes in Houston, ACT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Atlanta

Popular Test Prep

GMAT Test Prep in Washington DC, SAT Test Prep in Denver, SSAT Test Prep in Seattle, GMAT Test Prep in Houston, ISEE Test Prep in New York City, GRE Test Prep in Houston, MCAT Test Prep in Boston, GMAT Test Prep in New York City, ACT Test Prep in Seattle, MCAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : How to find the common factors of squares

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #1 : Factoring And Simplifying Square Roots

Example Question #51 : Simplifying Square Roots

Example Question #21 : Basic Squaring / Square Roots

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: