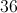All PSAT Math Resources
Example Questions
Example Question #1 : How To Find A Ratio Of Exponents
If 



Possible Answers:
Correct answer:
Explanation:
43 = 64
Alternatively written, this is 4(4)(4) = 64 or 43 = 641.
Thus, m = 3 and n = 1.
m/n = 3/1 = 3.
Example Question #2 : How To Find A Ratio Of Exponents
Write the following logarithm in expanded form:
Possible Answers:
Correct answer:
Explanation:
Example Question #10 : How To Find An Exponent From A Rational Number
Which of the following lists the above quantities from least to greatest?
Possible Answers:
IV, III, II, I
I, III, II, IV
II, III, I, IV
I, IV, II, III
I, IV, III, II
Correct answer:
I, III, II, IV
Explanation:
Example Question #1 : Exponential Ratios And Rational Numbers
Solve for 
Possible Answers:
Correct answer:
Explanation:
Since
Hence
Example Question #2 : How To Find An Exponent From A Rational Number
Simplify:
Possible Answers:
Correct answer:
Explanation:
Example Question #3 : How To Find An Exponent From A Rational Number
Solve for 
Possible Answers:
Correct answer:
Explanation:
From the equation one can see that
Hence 
Example Question #4 : How To Find An Exponent From A Rational Number
Evaluate:
Possible Answers:
Correct answer:
Explanation:
Example Question #541 : Algebra
Solve for 
Possible Answers:
Correct answer:
Explanation:
Example Question #542 : Algebra
and
Find
Possible Answers:
Correct answer:
Explanation:
Hence the correct answer is 
Example Question #543 : Algebra
Solve for 
Possible Answers:
Correct answer:
Explanation:
Use the rules of logarithms to combine terms.
Hence,
By fatoring we get
Hence 
However, you cannot take the logarithm of a negative number. Thus, the only value for 

Alisha
Certified Tutor
Certified Tutor
University of Wisconsin-Madison, Bachelor in Arts, Mathematics. University of South Florida-Main Campus, Master of Arts, Prem...
All PSAT Math Resources
Popular Subjects
LSAT Tutors in Miami, MCAT Tutors in Seattle, Spanish Tutors in Chicago, SSAT Tutors in Chicago, Calculus Tutors in Miami, SSAT Tutors in Houston, Calculus Tutors in Los Angeles, GRE Tutors in Chicago, GMAT Tutors in San Diego, Chemistry Tutors in Denver
Popular Courses & Classes
GRE Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Boston, SSAT Courses & Classes in Boston, ISEE Courses & Classes in Houston, SAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Denver, LSAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Denver, SSAT Courses & Classes in Phoenix, SAT Courses & Classes in Atlanta









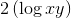














![\sqrt[3]{x^{10}y^{8}z^{9}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25511/gif.latex)
![x^{3}y^{2}z^{3}\sqrt[3]{xy^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/31984/gif.latex)
![x^{3}y^{2}z^{3}^{\sqrt[3]{xyz}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/31987/gif.latex)


![\sqrt[3]{xy^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/31988/gif.latex)
![\sqrt[3]{x^{9}xy^{6}y^{2}z^{9}}=x^{3}y^{2}z^{3}\sqrt[3]{xy^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/109415/gif.latex)