All PSAT Math Resources
Example Questions
Example Question #1 : Venn Diagrams
Given the Venn diagram below, which of the following does not belong to 
The symbol 

Example Question #1 : How To Find The Union Of A Venn Diagram
Sixty high school seniors were polled to see if they were taking history and calculus. A total of 29 students said they were taking calculus, and a total of 50 students said they were taking history. What is the minimum number of students who take both history and calculus?
We can draw a Venn diagram to see these two sets of students.

We need to find the overlap between these two sets. To find that, add up the total number of students who are taking history and the total number of students who are taking calculus.
Notice that we have more students this way than the total number who were polled. That is because the students who are taking history AND calculus have been double counted. Subtract the total number of students polled to find out how many students were counted twice.
Example Question #1 : Venn Diagrams

A group of high school juniors are taking Biology, Calculus, and Spanish as shown above. Which student is not in the set 
Bob
Steph
Andy
Patrick
Molly
Patrick
The notation 

Example Question #11 : How To Find The Union Of A Venn Diagram
Forty students play soccer and/or basketball after school. Twenty-four students play soccer and twenty-nine play basketball. How many students play both soccer and basketball?
We can draw a Venn diagram of these students.

Drawn this way, there are more students on the Venn diagram than we have.
This is because some of the students play both sports and should be in the overlap on the Venn diagram. To find the number of students in the overlap, subtract the total number of students given from the number on the diagram.
This represents the number of students who were counted twice, or the number in the overlap.
We can redraw the correct Venn diagram with this number.

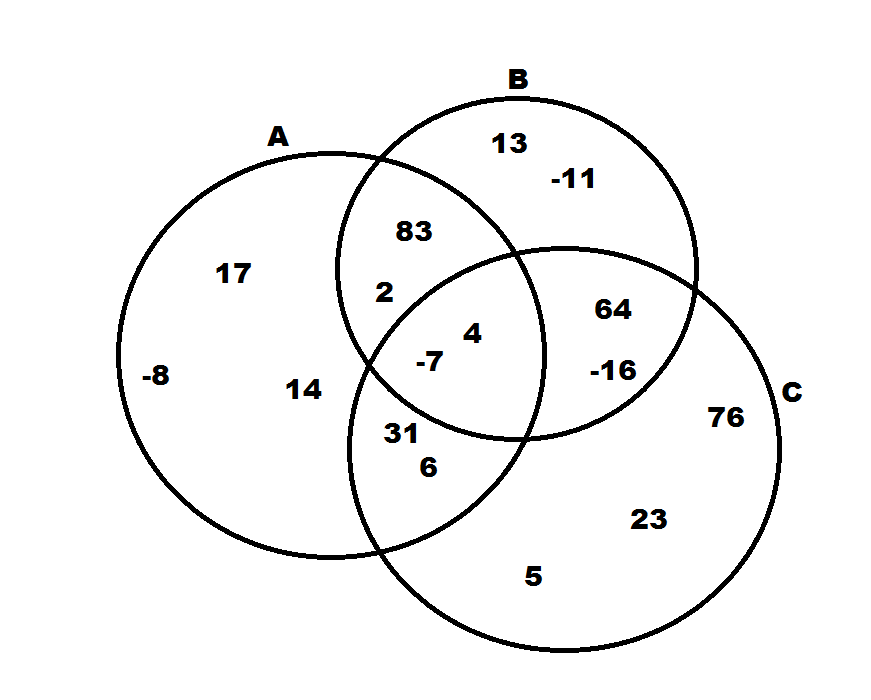
Example Question #11 : Data Analysis

Giving the Venn diagram above, what is the sum of the numbers in the set 
The notation 


When we add the numbers together, we get:
Example Question #12 : How To Find The Union Of A Venn Diagram
In a class of senior high-school students, 



A Venn diagram can help us determine the total number of students in the class.
First, we must calculate the number of students who have ONLY cats or ONLY dogs. First, for cats, 15 students have cats, and 5 students have both cats and dogs.
Ten students have only cats.
For dogs, 12 students have dogs, and 5 students have both cats and dogs.
Seven students have only dogs.
Using this information, we can fill in the Venn diagram.

This diagram shows the 10 students with only cats, the 7 students with only dogs, the 5 students with both, and the 8 students with neither. Adding up the numbers will give us the total number of students.
Example Question #1 : How To Find The Probability Of An Outcome
A bag of marbles has 7 yellow marbles, 5 red marbles, 3 blue marbles, and 6 white marbles. What is the probability of choosing a yellow marble, putting it back and choosing a blue marble, and then NOT putting the blue marble back and picking a white marble?
1/70
1/9
3/17
8/31
2/3
1/70
There are a total of 7 + 5 + 3 + 6 = 21 marbles. The probability of picking a yellow marble is 7/21 = 1/3. Then we put it back and choose a blue marble with probability 3/21 = 1/7. We do NOT put this blue marble back, but then we grab for a white. The probability of picking a white is now 6/20 = 3/10, because now we are choosing from 20 marbles instead of 21. So putting it together, the probability of choosing a yellow marble, replacing it and then choosing a blue and a white, is 1/3 * 1/7 * 3/10 = 1/70.
Example Question #111 : Data Analysis
A bag of jellybeans has 20 watermelon jellybeans, 45 sour apple jellybeans, 30 orange jellybeans and 5 cotton candy jellybeans. If you reach in and grab one jelly bean, what is the probability that it will be watermelon flavored?
1/5
1/20
1/3
4/19
1/4
1/5
Add up the total number of jellybeans, 20 + 45 + 30 + 5 = 100.
Divide the number of watermelon jellybeans by the total: 20/100 and reduce the fraction to 1/5.
Example Question #1 : How To Find The Probability Of An Outcome
You went to order a cake but all of the cakes are in identical boxes. If there are five chocolate cakes, four carrot cakes, three vanilla cakes, and six red velvet cakes, what is the maximum number of boxes that you would have to open to ensure that you have one of each type of cake?
4
16
12
9
16
There are four different types of cake. In this type of problem we want to guarantee we have one of each, so we need to assumbe we have very bad luck. We start with the red velvet since that is the type with the most cakes. If we open those 6 we are not guaranteed to have different ones. Then say we opened all five chocolate cakes, then all four carrot cakes. We still have only three types of cakes but opened 15 boxes. When we open the next box (16) we will be guaranteed to have one of each.
Example Question #1 : Probability
A circle is inscribed inside a square. If a point inside the square is selected at random, what is the probability that the point will also be inside the circle?
3/4
π/4
5/6
π/6
π/4
The probability of the point being inside the circle is the ratio of the area of the circle to the area of the square. If we suppose that the circle has radius r, then the square must have side 2r. The area of the circle is πr2 and the area of the square is 〖(2r)〗2=〖4r〗2, so the proportion of the areas is (πr2)/〖4r〗2 =π/4.
All PSAT Math Resources





































