All PSAT Math Resources
Example Questions
Example Question #11 : Algebraic Fractions
Which of the following provides the complete solution set for 
No solutions
The absolute value will always be positive or 0, therefore all values of z will create a true statement as long as 
Example Question #51 : Algebraic Fractions
If the average (arithmetic mean) of 






There is not enough information to determine the answer.
If we can find the sum of 




Write out the average formula for the original three quantities. Remember, adding together and dividing by the number of quantities gives the average:
Isolate 
Write out the average formula for the new three quantities:
Combine the integers in the numerator:
Replace 
Example Question #1 : How To Find Excluded Values
Find the excluded values of the following algebraic fraction
The numerator cancels all the binomials in the denomniator so ther are no excluded values.
To find the excluded values of a algebraic fraction you need to find when the denominator is zero. To find when the denominator is zero you need to factor it. This denominator factors into
so this is zero when x=4,7 so our answer is
Example Question #1 : How To Find Inverse Variation
A school's tornado shelter has enough food to last 20 children for 6 days. If 24 children ended up taking shelter together, for how many fewer days will the food last?
8
6
1
4
2
1
Because the number of days goes down as the number of children goes up, this problem type is inverse variation. We can solve this problem by the following steps:
20*6=24*x
120=24x
x=120/24
x=5
In this equation, x represents the total number of days that can be weathered by 24 students. This is down from the 6 days that 20 students could take shelter together. So the difference is 1 day less.
Example Question #2 : How To Find Inverse Variation


If 





If 



Substitute 

This rounds to 2.3.
Example Question #2 : How To Find Inverse Variation


If 




If 



Substitute 

Example Question #2 : How To Find Inverse Variation
Find the inverse of
To find the inverse we first switch the x and y variables
Now we add 4 to each side
From here to isolate y we need to multiply each side by 2
By distributing the 2 we get our final solution:
Example Question #2 : How To Find Inverse Variation


If 



If 




Substitute 

This rounds to 3.5.
Example Question #2 : How To Find Inverse Variation


If 



If 




Substitute 

Example Question #3 : How To Find Inverse Variation
Find the inverse of 
To find the inverse of a function we need to first switch the 


We now solve for y by subtracting 1 from each side
From here we divide both sides by 2 which results in
Certified Tutor
Certified Tutor
All PSAT Math Resources






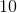


























![A'\sqrt[3]{B'} = A\sqrt[3]{B}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/230538/gif.latex)
![A'\sqrt[3]{100} = 8\sqrt[3]{66}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/230541/gif.latex)
![A'=\frac{ 8\sqrt[3]{66}}{\sqrt[3]{100} } \approx \frac{ 8 \cdot 4.0412}{4.6416} \approx 7.0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/230542/gif.latex)































