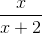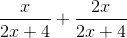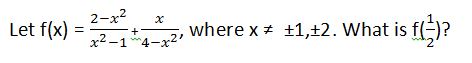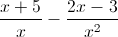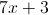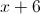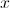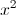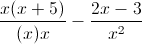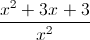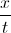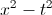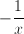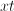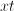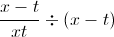Begin by putting the equation given into your own words. It might sound something similar to:

2 times x squared plus 7

Now, go through each answer choice and see if any of them are similar to this. We immediately see that the answer "7 more than 2 times the square of x" is similar to what we came up with. Let's do a quick run through of the other choices to be sure of our choice: 

"2 times 7 more than the square of x" is equal to \(\displaystyle \small 2(x^2+7)\), which is equivalent to \(\displaystyle \small 2x^2+14\). 

"2 times 7 less than the square of x" is equal to \(\displaystyle \small \small 2(x^2-7)\), which is equivalent to \(\displaystyle \small \small 2x^2-14\).

"7 more than the square of 2x" is equal to \(\displaystyle \small (2x)^2+7\), which is equivalent to \(\displaystyle \small 4x^2+7\).

"7 less than the square of 2x" is equal to \(\displaystyle \small \small (2x)^2-7\), which is equivalent to \(\displaystyle \small \small 4x^2-7\).

The only answer that works is "7 more than 2 times the square of x". This is the correct answer.

When solving a complex expression, remember the acronym PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction). Reading left to right, begin by doing all operations within the innermost Parentheses first:

\(\displaystyle (-3(2+3))-4(3(2^2))\)

\(\displaystyle =(-3(5))-4(3(4))\)

\(\displaystyle =(-15)-4(12)\)

Continue simplifying using the acronym PEMDAS:

\(\displaystyle =-15-48\)

\(\displaystyle =-63\)

The expression is equal to -63.

\(\displaystyle \frac{2x-3}{x+2}+\frac{5x-6}{x+2}\)

Same denominator means you add straight across the numerators, keeping the denominator the same.

\(\displaystyle \frac{2x-3+5x-6}{x+2}\)

Add like terms. 

\(\displaystyle \frac{2x+5x+3-6}{x+2}\)

Final Answer. 

\(\displaystyle \frac{7x-3}{x+2}\)

\(\displaystyle \frac{x^{2}-4}{2x+8}+\frac{-12}{2x+8}\)

Check for same Denominator

\(\displaystyle \frac{x^{2}-4+(-12)}{2x+8}\)

Add like terms 

\(\displaystyle \frac{x^{2}-16}{2x+8}\)

Check for GCF or if the expression can be factored

\(\displaystyle \frac{(x-4)(x+4)}{2(x+4)}\)

After factoring, divide out like terms. \(\displaystyle x+4\)

\(\displaystyle \frac{(x-4)}{2}\)

Final Answer

Since both expressions have a common denominator, x², we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.

To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.

\(\displaystyle \frac{x}{2x+4}+\frac{x}{x+2}\)

\(\displaystyle \frac{x}{2x+4}+\frac{(2)x}{(2)(x+2)}\)

\(\displaystyle \frac{x}{2x+4}+\frac{2x}{2x+4}\)

\(\displaystyle \frac{3x}{2x+4}\)

This is the most simplified version of the rational expression.

If we plug in a² for b in the radical expression, we get √(a³) = 8. This can be rewritten as a^3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer. 

\(\displaystyle \frac{x+5}{x}-\frac{2x-3}{x^{2}}\)

Determine an LCD (Least Common Denominator) between \(\displaystyle x\) and \(\displaystyle x^{2}\).

LCD = \(\displaystyle x^{2}\)

\(\displaystyle \frac{x(x+5)}{(x)x}-\frac{2x-3}{x^{2}}\)

Multiply the top and bottom of the first rational expression by \(\displaystyle x\), so that the denominator will be \(\displaystyle x^{2}\).

Distribute the \(\displaystyle x\) to \(\displaystyle x+5\).

\(\displaystyle \frac{x^{2}+5x}{x^{2}}-\frac{2x-3}{x^{2}}\)

Now you can subtract because both rational expressions have the same denominators.

\(\displaystyle \frac{x^{2}+5x-2x+3}{x^{2}}\)

Final Answer. 

\(\displaystyle \frac{x^{2}+3x+3}{x^{2}}\)

We will need to simplify the expression \(\displaystyle \frac{(\frac{1}{t}-\frac{1}{x})}{x-t}\). We can think of this as a large fraction with a numerator of \(\displaystyle \frac{1}{t}-\frac{1}{x}\) and a denominator of \(\displaystyle \dpi{100} x-t\).

In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. \(\displaystyle \frac{1}{t}\) has a denominator of \(\displaystyle \dpi{100} t\), and \(\displaystyle \dpi{100} -\frac{1}{x}\) has a denominator of \(\displaystyle \dpi{100} x\). The least common denominator that these two fractions have in common is \(\displaystyle \dpi{100} xt\). Thus, we are going to write equivalent fractions with denominators of \(\displaystyle \dpi{100} xt\).

In order to convert the fraction \(\displaystyle \dpi{100} \frac{1}{t}\) to a denominator with \(\displaystyle \dpi{100} xt\), we will need to multiply the top and bottom by \(\displaystyle \dpi{100} x\).

\(\displaystyle \frac{1}{t}=\frac{1\cdot x}{t\cdot x}=\frac{x}{xt}\)

Similarly, we will multiply the top and bottom of \(\displaystyle \dpi{100} -\frac{1}{x}\) by \(\displaystyle \dpi{100} t\).

\(\displaystyle \frac{1}{x}=\frac{1\cdot t}{x\cdot t}=\frac{t}{xt}\)

We can now rewrite \(\displaystyle \frac{1}{t}-\frac{1}{x}\) as follows:

\(\displaystyle \frac{1}{t}-\frac{1}{x}\) = \(\displaystyle \frac{x}{xt}-\frac{t}{xt}=\frac{x-t}{xt}\)

Let's go back to the original fraction \(\displaystyle \frac{(\frac{1}{t}-\frac{1}{x})}{x-t}\). We will now rewrite the numerator:

\(\displaystyle \frac{(\frac{1}{t}-\frac{1}{x})}{x-t}\) = \(\displaystyle \frac{\frac{x-t}{xt}}{x-t}\)

To simplify this further, we can think of \(\displaystyle \frac{\frac{x-t}{xt}}{x-t}\) as the same as \(\displaystyle \frac{x-t}{xt}\div (x-t)\) . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, \(\displaystyle a\div b=a\cdot \frac{1}{b}\).

\(\displaystyle \frac{x-t}{xt}\div (x-t)\) = \(\displaystyle \frac{x-t}{xt}\cdot \frac{1}{x-t}\)\(\displaystyle =\frac{x-t}{xt(x-t)}\)\(\displaystyle = \frac{1}{xt}\)

Lastly, we will use the property of exponents which states that, in general, \(\displaystyle \frac{1}{a}=a^{-1}\).

\(\displaystyle \frac{1}{xt}=(xt)^{-1}\)

The answer is \(\displaystyle (xt)^{-1}\).