All Precalculus Resources
Example Questions
Example Question #1 : Trigonometric Identities
Use trigonometric identities to solve the following equation for 
Use the trigonometric identities to switch sec into terms of tan:
hence,
So we have 
Therefore the solution is 
Example Question #1 : Solving Trigonometric Equations And Inequalities
Which of the following is not a solution to 
We begin by setting the right side of the equation equal to 0.
The equation might be easier to factor using the following substitution.
This gives the following
This can be factored as follows
Therefore
Replacing our substitution therefore gives
Within our designated domain, we get three answers between our two equations.


Therefore, the only choice that isn't correct is
Example Question #2 : Solving Trigonometric Equations And Inequalities
Find one possible value of 
Begin by isolating the tangent side of the equation:
Next, take the inverse tangent of both sides:
Divide by five to get the final answer:
Example Question #3 : Solving Trigonometric Equations And Inequalities
Use trigonometric identities to solve for the angle value.
There are two ways to solve this problem. The first involves two trigonometric identities:
The second method allows us to only use the first trigonometric identity:
Example Question #4 : Solving Trigonometric Equations And Inequalities
Use trigonometric identities to solve the equation for the angle value.
The simplest way to solve this problem is using the double angle identity for cosine.
Substituting this value into the original equation gives us:
Example Question #213 : Pre Calculus
According to the trigonometric identities,
The trigonometric identity 
Some other identities that are important to know are:
Example Question #1 : Solve Trigonometric Equations And Inequalities In Quadratic Form
If 
![\left[0,\frac{\pi}{2}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/357853/gif.latex)
Factorize 
Set both terms equal to zero and solve.
This value is not within the ![[0,\frac{\pi}{2}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/357296/gif.latex)
This is the only correct value in the ![[0,\frac{\pi}{2}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/357300/gif.latex)
Example Question #2 : Solving Trigonometric Equations And Inequalities
Solve for 


If you substitute 


Then we can plug 

Example Question #2 : Solve Trigonometric Equations And Inequalities In Quadratic Form
Given that theta exists from ![[0,2\pi]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/363051/gif.latex)
In order to solve 

Substract 
Factor the left side of the equation.
Set each term equal to zero, and solve for theta with the restriction ![[0,2\pi]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/363058/gif.latex)
The correct answer is:
Example Question #12 : Trigonometric Identities
Solve 
There is no solution.
There is no solution.
By subtracting 

Certified Tutor
All Precalculus Resources



















































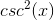






























![cos(\theta)[2cos(\theta)-1]=0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/363057/gif.latex)














