Rewrite  in slope-intercept form, , to determine the slope.

The slope of the given function is 2.

Substitute the slope and the given point, , in the slope-intercept form to determine the y-intercept.

Substitute this and the slope back to the slope-intercept equation.

The equation of the tangent line is:  

We begin by finding the equation of the derivative using the limit definition:

We define  and  as follows:

We can then define their difference:

Then, we divide by h to prepare to take the limit:

Then, the limit will give us the equation of the derivative.

Now, we must realize that the slope of the line tangent to the curve at the given point is equivalent to the derivative at the point. So if we define our tangent line as: , then this m is defined thus:

Therefore, the equation of the line tangent to the curve at the given point is:

First, find the slope of this tangent line by taking the derivative:

Plugging in 1 for x:

So the slope is 4

Now we need to find the y-coordinate when x is 1, so plug 1 in to the original equation:

To write the equation, use point-slope form and then use algebra to change to slope-intercept like the answer choices:

distribute the 4

add 2 to both sides

First, find the slope of the tangent line by taking the first derivative:

To finish determining the slope, plug in the x-value, 2:

the slope is 6

Now find the y-coordinate where x is 2 by plugging in 2 to the original equation:

To write the equation, start in point-slope form and then use algebra to get it into slope-intercept like the answer choices.

distribute the 6

add 8 to both sides

First, take the first derivative in order to find the slope:

To continue finding the slope, plug in the x-value, -2:

Then find the y-coordinate by plugging -2 into the original equation:

The y-coordinate is

Now write the equation in point-slope form then algebraically manipulate it to match one of the slope-intercept forms of the answer choices.

distribute the -5

add to both sides

First distribute the . That will make it easier to take the derivative:

Now take the derivative of the equation:

To find the slope, plug in the x-value -3:

To find the y-coordinate of the point, plug in the x-value into the original equation:

Now write the equation in point-slope, then use algebra to get it into slope-intercept like the answer choices:

 distribute

subtract from both sides

write as a mixed number

 will approach when approaches , so  will be of type  as shown below:

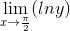
So, we can apply the L’ Hospital's Rule:

since:

hence:

When x=3/2 our denominator is zero so we can't just plug in 3/2 to get our limit. If we look at the numerator when x=3/2 we find that it is zero as well so our numerator can be factored. We see that our limit can be re-written as:

we then can cancel the 2x-3 from the numerator and denominator leaving us with:

and we can just plug in 3/2 into this limit to get 

note: our function is not continuous at x=3/2 but the limit does exist.

To solve this problem we need to expand the term in the numerator 

when we do that we get 

the second degree x terms cancel and we get

now we can cancel our h's in the numerator and denominator to get

then we can just plug 0 in for h and we get our answer

The function has a removable discontinuity at  .  Once a factor of  is "divided out" the resultant function is , which evaluates to  as  approaches 0.