All Precalculus Resources
Example Questions
Example Question #191 : Pre Calculus
At what value of 

There is no hole
To find discontinuity we need to look at where the denominator of the function is equal to zero. Looking at our function,

we need to set the denominator equal to zero and solve for 
When 

Therefore 
Example Question #1 : Limits
What is the

The limit does not exist
Means to find the limit of the function as 






Example Question #2 : Limits
What is the

The limit does not exist
We first need to simplify the function, we can do this by factoring the numerator and denominator.
If we plug in 3 into the simplified function, we get:
Example Question #2 : Limits
What is the

Substituting 

Example Question #5 : Introductory Calculus
Evaluate the following:
limit does not exist
When evaluating limits at infinity there are three rules to keep in mind:
- If the degree of the highest exponent in the numerator is equal to the degree of the highest exponent in the denominator, then the limit is equal to the ratio of the coefficient of the highest exponent in the numerator over the coefficient of the highest exponent in the denominator. Make sure to include signs.
- If the degree of the highest exponent in the numerator is less than the degree of the highest exponent in the denominator, the limit = 0.
- If the degree of the highest exponent in the numerator is greater than the degree of the higest exponent in the denominator, divide the highest power in the numerator by the highest power in the denominator and substitute for inifity. You will either subsitute for positive or negative infinity based on what the questions asks you to evaluate the limit at.
In this case, the degree is higher in the numerator than the denominator (rule #3). Hence, you need to divide the highest powers and evaluate.
Evaluate 
Answer: limit =
Example Question #6 : Introductory Calculus
Evaluate the following:
When evaluating limits at infinity there are three rules to keep in mind:
- If the degree of the highest exponent in the numerator is equal to the degree of the highest exponent in the denominator, then the limit is equal to the ratio of the coefficient of the highest exponent in the numerator over the coefficient of the highest exponent in the denominator. Make sure to include signs.
- If the degree of the highest exponent in the numerator is less than the degree of the highest exponent in the denominator, the limit = 0.
- If the degree of the highest exponent in the numerator is greater than the degree of the higest exponent in the denominator, divide the highest power in the numerator by the highest power in the denominator and substitute for inifity. You will either subsitute for positive or negative infinity based on what the questions asks you to evaluate the limit at.
In this case, the both the numerator and denominator have the highest degree of an exponent of 4 (rule #1). Hence, you need to compare the ratio of the coefficients.
Answer: limit =
Example Question #1 : Limits
What is the,

The end behavior of the function 

Now we take the

Thus the limit of our original function is also 
Example Question #3 : Limits
Evaluate the limit below:
1
0




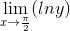

So, we can apply the L’ Hospital's Rule:
since:
hence:
Example Question #1 : Limits
Find the limit
When x=3/2 our denominator is zero so we can't just plug in 3/2 to get our limit. If we look at the numerator when x=3/2 we find that it is zero as well so our numerator can be factored. We see that our limit can be re-written as:
we then can cancel the 2x-3 from the numerator and denominator leaving us with:
and we can just plug in 3/2 into this limit to get
note: our function is not continuous at x=3/2 but the limit does exist.
Example Question #2 : Limits
Solve the following limit:
To solve this problem we need to expand the term in the numerator
when we do that we get
the second degree x terms cancel and we get
now we can cancel our h's in the numerator and denominator to get
then we can just plug 0 in for h and we get our answer
Certified Tutor
Certified Tutor
All Precalculus Resources










































































