First, we must solve for the roots of the cubic polynomial equation.

We obtain that the roots are .

Now there are four regions created by these numbers:

• . In this region, the values of the polynomial are negative (i.e.plug in  and you obtain 

• . In this region, the values of the polynomial are positive (when , polynomial evaluates to )

•  . In this region the polynomial switches again to negative.

• . In this region the values of the polynomial are positive

Hence the two regions we want are  and .

First, subtract  from both sides so you get 

.

Then find the common denominator and simplify 

.

Next, factor out the numerator 

and set each of the three factor equal to zero and solve for .

The solutions are 

.

Now plug in values between , , , and  into the inequality and observe if the conditions of the inequality are met.

Note that . They are met in the interval  and .

Thus, the solution to the inequality is  

. 

1) Multiply both sides of the equation by the common denominator of the fractions:

2) Simplify:

3) For standard notation, and the fact that inequalities can be read backwards:

     For interval notation:

4) Graph:

Graph the rational expression,

1) Because  and a divide by is undefined in the real number system, there is a vertical asymptote where .

2) As   ,   , and as  ,  .

3) As  ,  , and as   ,  .

4) The funtion y is exists over the allowed x-intervals:

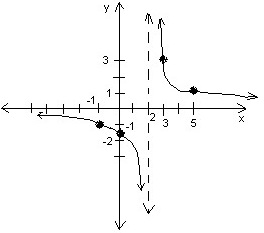
One approach for solving the inequality: 

For 

1) Determine where  over the x-values  or .

2)  for the intervals  or .

3) Then the solution is .

Another approach for solving the inequality:

1) Write   as , then determine the x-values that cause  to be true: 

2)  is true for  or .

3) Then the solution is .

When solving for a point where the function will be undefined, you set the denominator equal to zero and solve for .  This creates a vertical asymptote because when the denominator equals zero the function is undefined and we are solving for .  Say for example a function is undefined at .  So at all values of where this function is undefined creating a vertical asymptote.

We begin by finding the zeros of the equation using the numerator.

So we know that the function will equal zero when .  If we just look at the numerator of the function, then this graph would be a parabola with its point at .  Now we will solve for the points where the function is undefined by setting the denominator equal to zero and solving for .

 And so the function is undefined at .  If we make a table to solve for some of the points of the graph:

 And if we graph these points we see something like below (which is our answer).  Note that the dotted blue line is the vertical asymptote at .

The zeros of the function are the values of  where the function will be equal to zero.  In order to find these we set the numerator of the function equal to zero.

We only need to solve for  once,

So the zeros of this function are .

To solve for the points at which this function will be undefined, we set the denominator equal to zero and solve for .

And so the function is undefined at

This inequality wants all values where  is greater than .  So everything up until  is included and this is represented by having a dotted line on the graph or an open circle on a number line.

We will first begin by solving for the zeros and undefined points of the inequality.  We solve for the zeros by setting the numerator equal to zero.

And so the zeros of this function are at 

Now we will solve for the undefined points by setting the denominator equal to zero.  Since the denominator is , then whenever , the function is undefined.  Now we need to find for which values of  is each factor is greater than zero.

For , any value where  will be positive and we will be able to graph it.  For , any value where  will be positive.  Now, we can only graph these values up until  because the function is undefined here.  We are able to pick up the graph again once we reach .  The graph will look like the one below.

We begin by moving all of our terms to the left side of the inequality.

We then factor.

That means our left side will equal 0 when .  However, we also want to know the values when the left side is less than zero.  We can do this using test regions.  We begin by drawing a number line with our two numbers labeled.

We notice that our two numbers divide our line into three regions.  We simply need to try a test value in each region.  We begin with our leftmost region by selecting a number less than .  We then plug that value into the left side of our inequality to see if the result is positive or negative.  Any value (such as ) will give us a positive value.

We then repeat this process with the center region by selecting a value between our two numbers.  Any value (such as ) will result in a negative outcome.

Finally we complete the process with the rightmost region by selecting a value larger than .  Any value (such as ) will result in a positive value.

We then label our regions accordingly.

Since we want the result to be less than zero, we want the values between our two numbers.  However, since our left side can be less than or equal to zero, we can also include the two numbers themselves.  We can express this as