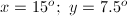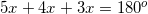Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Linear Functions

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Understanding Complementary And Suplmentary Angles

Solve for .

(Figure not drawn to scale).

Possible Answers:

12^o

10^o

8^o

14^o

Correct answer:

14^o

Explanation:

The angles are supplementary, therefore, the sum of the angles must equal 180^o .

$\small (4n+22^o)+(8n-10^o)=180^o$

$\small 4n+22^o+8n-10^o=180^o$

$\small 12n+12^o=180^o$

$\small 12n=168^o$

$\small n=14^o$

Report an Error

Example Question #2 : Understanding Complementary And Suplmentary Angles

Are $129^{\circ}$ and $51^{\circ}$ supplementary angles?

Possible Answers:

Yes

Not enough information

Correct answer:

Yes

Explanation:

Since supplementary angles must add up to $180^{\circ}$ , the given angles are indeed supplementary.

Report an Error

Example Question #1 : Finding Angles

Solve for and .

(Figure not drawn to scale).

Possible Answers:

$\small x=15^o;\ y=37.5^o$

$\small x=15^o;\ y=52.5^o$

$\small x=7.5^o;\ y=18.75^o$

$\small x=15^o;\ y=7.5^o$

Correct answer:

$\small x=15^o;\ y=37.5^o$

Explanation:

The angles containing the variable all reside along one line, therefore, their sum must be 180^o .

$\small 5x+4x+3x=180^o$

$\small 12x=180^o$

$\small x=15^o$

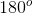
Because and are opposite angles, they must be equal.

$\small 2y=5x$

$\small x=15^o$

$\small 2y=5(15^o)=75^o$

$\small y=\frac{75^o}{2}=37.5^o$

Report an Error

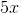
Example Question #1 : Graph A Linear Function

Which of the following could be the function modeled by this graph?

Linearfxn

Possible Answers:

y=7x-5

y=5x-7

y=5x+7

$y=\frac{1}{5}x-7$

Correct answer:

y=5x-7

Explanation:

Which of the following could be the function modeled by this graph?

Linearfxn

We can begin here by trying to identify a couple points on the graph

We can see that it crosses the y-axis at (0,-7)

Therefore, not only do we have a point, we have the y-intercept. This tells us that the equation of the line needs to have a in it somewhere. Eliminate any option that do not have this feature.

Next, find the slope by counting up and over from the y-intercept to the next clear point.

It seems like the line goes up 5 and right 1 to the point (1,-2)

This means we have a slope of 5, which means our equation must look like this:

y=5x-7

Report an Error

Example Question #1 : Graph A Linear Function

Find the slope of the linear function

y-3=5(x+2)

Possible Answers:

m=2

m=-3

m=3

m=5

Correct answer:

m=5

Explanation:

For the linear function in point-slope form

$y-y_{1}=m\left ( x-x_{1}\right )$

The slope is equal to

For this problem

y-3=5(x+2)

we get

m=5

Report an Error

Example Question #2 : Graph A Linear Function

Find the slope of the linear function

y-7=10(x+1)

Possible Answers:

m=-7

m=1

m=10

m=7

Correct answer:

m=10

Explanation:

For the linear function in point-slope form

$y-y_{1}=m\left ( x-x_{1}\right )$

The slope is equal to

For this problem

y-7=10(x+1)

we get

m=10

Report an Error

Example Question #3 : Linear Functions

What is the y-intercept of the line below?

y = 3x + 4

Possible Answers:

(3,0)

(0, 4)

(4,0)

(0, -3)

(0, 3)

Correct answer:

(0, 4)

Explanation:

By definition, the y-intercept is the point on the line that crosses the y-axis. This can be found by substituting x = 0 into the equation. When we do this with our equation,

$y = 3x + 4 = 3\cdot0 + 4 = 0 + 4 = 4$ .

Alternatively, you can remember y = mx + b form, a general form for a line in which is the slope and is the y-intercept.

Report an Error

Example Question #4 : Linear Functions

What is the slope of the line below?

$y = \frac{2}{3}x + 6$

Possible Answers:

$\frac{1}{6}$

$-\frac{2}{3}$

$\frac{2}{3}$

Correct answer:

$\frac{2}{3}$

Explanation:

Recall slope-intercept form, or y = mx + b . In this form, is the slope and is the y-intercept. Given our equation above, the slope must be the coefficient of the x, which is $\frac{2}{3}$ .

Report an Error

Example Question #5 : Linear Functions

What is the x-intercept of the equation below?

y = 3x - 6

Possible Answers:

(0, -6)

$(\frac{1}{2}, 0)$

(-2, 0)

(0, 2)

(2,0)

Correct answer:

(2,0)

Explanation:

The x-intercept of an equation is the point at which the line crosses the x-axis. Thus, we can find the x-intercept by plugging in y=0 . When we do this with our equation:

$y = 3x - 6 \rightarrow 0 = 3x - 6\rightarrow6 = 3x \rightarrow2 = x$

Thus, our x-intercept is the point (2,0) .

Report an Error

Example Question #1 : Determine The Equation Of A Linear Function

What is the equation of the line that passes through the points (0,2) and (4,7) ?

Express your answer in y=mx+b form.

Possible Answers:

y =2

None of the other answers.

$y = \frac{5}{4}x+2$

y = 4x+2

$y = \frac{1}{2}x + 5$

Correct answer:

$y = \frac{5}{4}x+2$

Explanation:

First, we need to compute , the slope. We can do this with the slope formula

$m = \frac{y_2-y_1}{x_2-x_1}$ , sometimes called "rise over run"

$m = \frac{7-2}{4-0} = \frac{5}{4}$

So we now have

$y = \frac{5}{4}x +b$

Now in order to solve for we substitute one of our points into the equation we found. It doesn't matter which point we use, so we'll use (0,2) .

We then have:

$2 = \frac{5}{4}0 +b$

Which becomes 2 = b .

Hence we take our found value for and plug it back into $y= \frac{5}{4}x+b$ to get

$y =\frac{5}{4}x+2$ .

Report an Error

View Pre-Calculus Tutors

Blossom
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Computer Science.

View Pre-Calculus Tutors

Masoud
Certified Tutor

University of Guilan,, Bachelor of Science, Biological/Biosystems Engineering. University of Tehran, Master of Science, Anima...

View Pre-Calculus Tutors

Abhisek
Certified Tutor

University of Florida, Bachelor of Engineering, Computer Science.

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Dallas Fort Worth, ISEE Tutors in Seattle, Statistics Tutors in Los Angeles, Spanish Tutors in Dallas Fort Worth, LSAT Tutors in Atlanta, Calculus Tutors in Houston, Statistics Tutors in Houston, Computer Science Tutors in Dallas Fort Worth, Biology Tutors in Seattle, Spanish Tutors in Seattle

Popular Courses & Classes

Spanish Courses & Classes in Phoenix, LSAT Courses & Classes in Atlanta, LSAT Courses & Classes in Miami, ACT Courses & Classes in Philadelphia, Spanish Courses & Classes in Philadelphia, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in New York City, MCAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Boston, ISEE Courses & Classes in Atlanta

Popular Test Prep

GMAT Test Prep in Boston, LSAT Test Prep in New York City, ACT Test Prep in Philadelphia, SSAT Test Prep in Philadelphia, SSAT Test Prep in Miami, ISEE Test Prep in Seattle, SAT Test Prep in Dallas Fort Worth, SAT Test Prep in Washington DC, ISEE Test Prep in Houston, ISEE Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Linear Functions

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #1 : Understanding Complementary And Suplmentary Angles

Example Question #2 : Understanding Complementary And Suplmentary Angles

Example Question #1 : Finding Angles

Example Question #1 : Graph A Linear Function

Example Question #1 : Graph A Linear Function

Example Question #2 : Graph A Linear Function

Example Question #3 : Linear Functions

Example Question #4 : Linear Functions

Example Question #5 : Linear Functions

Example Question #1 : Determine The Equation Of A Linear Function

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: