will approach when approaches , so  will be of type  as shown below:

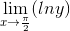
So, we can apply the L’ Hospital's Rule:

since:

hence:

When x=3/2 our denominator is zero so we can't just plug in 3/2 to get our limit. If we look at the numerator when x=3/2 we find that it is zero as well so our numerator can be factored. We see that our limit can be re-written as:

we then can cancel the 2x-3 from the numerator and denominator leaving us with:

and we can just plug in 3/2 into this limit to get 

note: our function is not continuous at x=3/2 but the limit does exist.

To solve this problem we need to expand the term in the numerator 

when we do that we get 

the second degree x terms cancel and we get

now we can cancel our h's in the numerator and denominator to get

then we can just plug 0 in for h and we get our answer

The function has a removable discontinuity at  .  Once a factor of  is "divided out" the resultant function is , which evaluates to  as  approaches 0.

This is a graph of . We know that  is undefined; therefore, there is no value for . But as we take a look at the graph, we can see that as  approaches 0 from the left,  approaches negative infinity. 

This can be illustrated by thinking of small negative numbers.

NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful. 

 is actually infinity, not negative infinity. 

This can be rewritten as follows:

We can substitute , noting that as , : 

, which is the correct choice.

As x approaches infinity we only need to look at the highest order of polynomial in both the numerator and denominator. Then we compare the highest order polynomial in both the numerator and denominator. If the denominator is higher order our limit goes to zero, if the numerator is higher our order our limit goes to positive or negative infinity (depending on the sign of the highest order x term). If our numerator and denominator have the same order the limit goes to a/b where a is the coefficient for the highest order x in the numerator and b is the coefficient for the highest order x in the denominator. 

Our numerator has higher order and the coefficient for the x to the fourth term is negative so our limit goes to negative infinity. 

As x approaches infinity we only need to look at the highest order of polynomial in both the numerator and denominator. Then we compare the highest order polynomial in both the numerator and denominator. If the denominator is higher order our limit goes to zero, if the numerator is higher our order our limit goes to positive or negative infinity (depending on the sign of the highest order x term). If our numerator and denominator have the same order the limit goes to a/b where a is the coefficient for the highest order x in the numerator and b is the coefficient for the highest order x in the denominator. 

For our equation the orders are the same in x for the numerator and denominator (both 4). So we divide the coefficients of the highest order x terms to get our limit and we get

The function given is a polynomial with a term , such that  is greater than 1. 

Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as  approaches infinity.

This tells us that the given function is not a very realistic description of a car's speed for large !

First factor the numerator to simplify the function.

,

so

.

Now

.

There is no denominator now, and hence no discontinuity.  The limit can be found by simply plugging in  for .

.