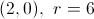All Precalculus Resources
Example Questions
Example Question #1 : Pre Calculus
What is the center and radius of the circle indicated by the equation?
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 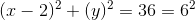


Example Question #1 : Circles
What is the equation of the circle with center at (4, -5) and a point on the circle at (4, -2)? What is the radius?
The form most often used for circles is the following general equation:

where (h, k) are the coordinates of the center and r is the radius. We are given the coordinates of the center as (4, -5), so h is 4 and k is -5.
We still need to find the radius. We can do this by plugging in the second given point, (4, -2).
Hence the formula of the circle is

and the radius is 
Example Question #1 : Conic Sections
Find the center and radius of this circle:


To solve this problem we need to get our function into the form:
where center=(h,k) and r=radius. To do this we need to complete the square with both the x an y parts of the equation
then we factor our trinomials and add our constants and we get:
so our center is 
Example Question #1 : Conic Sections
Which function will graph a circle of radius 

The general form for the function of a circle of radius r and centered at (a,b) is:

The circle is centered at 







The final form should be:

Example Question #1 : Determine The Equation Of A Circle In Standard Form
Write an equation for a circle.
Determine the equation for a circle in standard form with a radius of 

The standard form for the equation of a circle with radius 


Here, 

Note: one way to think of this equation is to remember the Pythagorean Theorem.
If the center is at the origin then the equation is

This describes a right triangle for any x and y that satisfy this equation. Here r is the hypotenues, but when all values of x and y are used it stays the same and the points map out a circle with radius r.
The rules of graph translation apply in the same way as with any function. That is they move the origin in the opposite direction by a and/or b.
Example Question #2 : Determine The Equation Of A Circle In Standard Form
Determine the equation of the circle in standard form from its graph.

The center of the circle is 
Find the horizontal distance from the center to the edge of the circle. At the center 



Plug these values: 
This gives

Example Question #2 : Circles
Express the following equation for a circle in standard form:
Remember that the standard form for the equation of a circle is given by the following formula:
Where the point (h,k) gives the center of the circle, and r is the radius. We can see from the form in which the equation is expressed in the problem that the only thing different with our form is that the terms on the left side of the equation are divided by 4. With some algebra, we'll multiply both sides by 4 to eliminate the 4's from the left side of equation:
Now we can see that our equation is the same as the formula for a circle in standard form, where (h,k) is (3,-2) and r=4.
Example Question #3 : Circles
Which of the following is an equation for a circle written in standard form?
Remember that in order for the equation of a circle to be in standard form, it must be written in the following way:
Where the point (h,k) tells us where the center of the circle is, and r is the radius of the circle. From our answer choices, we can see that the following is the only equation in which there are no fractions and there is addition of terms and not subtraction, which means it is in the standard form shown above:
For this circle, the center would be at (2,-3), and the radius would be 3.
Example Question #5 : Circles
Write the equation for a circle centered at 

The equation for a circle in general is 








Now we can generalize the equation as
Example Question #6 : Circles
What is the equation of a circle with radius of 

Recall that the equation of a circle is 


In this case, we have 
Note the negatives in the formula and be careful simpilfying.
When we are done, we have:

which gives us our answer when simplified.
Certified Tutor
All Precalculus Resources