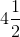The goal is to isolate the variable on one side.

\(\displaystyle \frac{1}{2}x+\frac{3}{4}=9\)

Subtract \(\displaystyle \frac{3}{4 }\) from each side of the equation:

\(\displaystyle \frac{1}{2}x+\frac{3}{4}-\frac{3}{4}=9-\frac{3}{4}\)

\(\displaystyle \frac{1}{2}x=8\frac{1}{4}\)

Multiply both sides by \(\displaystyle 2\):

\(\displaystyle x=16\frac{1}{2}\)

The goal is to isolate the variable to one side.

\(\displaystyle \frac{2}{3}x+6\frac{1}{3}=10\frac{1}{3}\)

First, convert mixed numbers to improper fractions:

\(\displaystyle \frac{2}{3}x+\frac{19}{3}=\frac{31}{3}\)

Subtract \(\displaystyle \frac{19}{3}\) from both sides:

\(\displaystyle \frac{2}{3}x+\frac{19}{3}-\frac{19}{3}=\frac{31}{3}-\frac{19}{3}\)

\(\displaystyle \frac{2}{3}x=\frac{12}{3}\)

Multiply each side by the reciprocal of \(\displaystyle \frac{2}{3}\):

\(\displaystyle \frac{3}{2}*\frac{2}{3}x=\frac{12}{3}*\frac{3}{2}\)

Cross out like terms and multiply:

\(\displaystyle \frac{1}{1}x=\frac{6}{1}*\frac{1}{1}\)

\(\displaystyle x=6\)

You are trying to isolate the \(\displaystyle \small x\). 

To do this you must first subtract both sides by 2 to get

\(\displaystyle \frac{1}{2}x=2\)

This then becomes a one-step problem where you multiply both sides by 2 to get

\(\displaystyle x=4\)

Once you've isolated x, it's important to find the lowest common denominator so that you can add the two fractions you're working with. 

Step 1: Isolate x and convert fractions so that they have a common denominator

\(\displaystyle x-\frac{1}{4}+\frac{1}{4}=\frac{1}{2}+\frac{1}{4}\)

\(\displaystyle x=\frac{1}{2}+ \frac{1}{4}=\frac{1\cdot 2}{2\cdot 2} +\frac{1}{4}=\frac{2}{4}+\frac{1}{4}\)

Step 2: solve for x

\(\displaystyle x=\frac{2}{4}+\frac{1}{4}=\frac{3}{4}, x=\frac{3}{4}\)

Cross multiplication is a short-cut that comes from multiplying by the denominators on both sides of an equation. Broken down, it works like this:

\(\displaystyle 4\cdot \frac{x}4=\frac{9}x\cdot 4{}{}\)

The 4's on the left side of the equation cancel out.

\(\displaystyle x=\frac{9\cdot 4}x{}\)

Now, do the same with the denominator on the right side.

\(\displaystyle x\cdot x=\frac{9\cdot 4}x\cdot x{}\)

The \(\displaystyle x\)'s on the right cancel out.

\(\displaystyle x\cdot x=9\cdot 4\)

This is simply the result of removing the denominators, then multiplying them on the opposite sides, i.e. cross multiplication.

Now, to finish solving for \(\displaystyle x\), simplify both sides.

\(\displaystyle x^{2}=36\)

Then take the square root to finish.

\(\displaystyle x=\sqrt{36}\)

\(\displaystyle x=\pm 6\)

\(\displaystyle \frac{2}{3}s+\frac{1}{3}=-\frac{1}{3}\)

\(\displaystyle \frac{2}{3}s+\frac{1}{3}-\frac{1}{3}=-\frac{1}{3}-\frac{1}{3}\)

\(\displaystyle \frac{2}{3}s=-\frac{2}{3}\)

\(\displaystyle \frac{3}{2}\cdot \left(\frac{2}{3}s\right)=\frac{3}{2}\cdot \left(-\frac{2}{3}\right)\)

\(\displaystyle s=-1\)

First, you want to leave all terms with x on one side and all other terms on the other side. To do this, we can subtract 4/3 from both sides. 

We now have 

\(\displaystyle \frac{2}{5}x = \frac{2}{3}\)

We can now multiply both sides by the reciprocal of 2/5, which is 5/2, to be able to solve for just x.

\(\displaystyle x = \frac{2}{3} * \frac{5}{2} = \frac{5}{3}\)

Explanation:

The goal is to isolate the variable to one side.

\(\displaystyle 1\frac{1}{3}x+7\frac{1}{3}=15\frac{1}{3}\)

First, convert the mixed numbers to improper fractions:

\(\displaystyle \frac{4}{3}x+\frac{22}{3}=\frac{46}{3}\)

Subtract \(\displaystyle \frac{22}{3}\)from both sides:

\(\displaystyle \frac{4}{3}x+\frac{22}{3}-\frac{22}{3}=\frac{46}{3}-\frac{22}{3}\)

\(\displaystyle \frac{4}{3}x=\frac{24}{3}\)

Multiply each side by the reciprocal of \(\displaystyle \frac{3}{4}\):

\(\displaystyle \frac{3}{4}*\frac{4}{3}x=\frac{24}{3}*\frac{3}{4}\)

\(\displaystyle x=6\)

1.) Add 8 to both sides, removing the "\(\displaystyle -8\)". It now reads \(\displaystyle \frac{1}{2}x=4x+7\)

2.) Multiply both sides by 2, removing the \(\displaystyle \frac{1}{2}\). It now reads \(\displaystyle x=8x+14\)

3.) Subtract \(\displaystyle 8x\) from both sides, removing the "\(\displaystyle 8x\)". It now reads \(\displaystyle -7x=14\)

4.) Divide both sides by "\(\displaystyle -7\)", resulting in \(\displaystyle x=-2\)