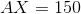Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Area of a Parallelogram

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Area Of A Parallelogram

What is the area of the parallelogram?

Problem_12

Possible Answers:

Correct answer:

Explanation:

The area of a parallelogram is determined using the equation:

A=bh

In this problem:

A=(7)(4)=28

Report an Error

Example Question #2 : Area Of A Parallelogram

Parallelogram

Refer to the above figure, which shows Parallelogram ABCD . You are given that $\overline{AX} \perp \overline{BC}$ and $\overline{AY} \perp \overline{CD}$ .

If you know the length of $\overline{AD}$ , then, of the following segments, choose the one whose length, if known, will allow us to calculate the area of Parallelogram ABCD .

Possible Answers:

$\overline{AX}$

$\overline{AB}$

$\overline{BC}$

$\overline{CD}$

$\overline{AY}$

Correct answer:

$\overline{AX}$

Explanation:

The area of a parallelogram is the product of the length of any one side, or its base, and the perpendicular distance to the opposite side, or its height. If we know $\overline{AD}$ , then we also know $\overline{BC}$ , which is of the same length. We can take $\overline{BC}$ to be the base, and the segement perpendicular to it, $\overline{AX}$ , as the altitude. Therefore, $\overline{AX}$ is the segment whose length we need to know.

Report an Error

Example Question #3 : Area Of A Parallelogram

Parallelogram

Note: Figure NOT drawn to scale.

Refer to the above figure, which shows Parallelogram ABCD . You are given that $\overline{AX} \perp \overline{BC}$ and $\overline{AY} \perp \overline{CD}$ .

AD = 100 , AB = 120 . AY = 80 .

Evaluate .

Possible Answers:

AX = 140

$AX = 66\frac{2}{3}$

AX = 150

AX = 60

AX = 96

Correct answer:

AX = 96

Explanation:

The area of a parallelogram is the product of the length of any one side, or its base, and the length of a segment perpendicular to that side, or its height.

One way to find the area is to multiply the length of side $\overline{CD}$ by its corresponding altitude, $\overline{AY}$ . Since CD = AB = 120 and AY = 80 ,

$A = (CD)(AY) = 120 \cdot 80 = 9,600$ .

Another way to find the area is to multiply the length of side $\overline{BC}$ by its corresponding altitude, $\overline{AX}$ . Since BC = AD= 100 and the area is 9,600, we set up this equation and solve for :

A = (BC)(AX)

$100 \cdot AX =9,600$

AX = 96

Report an Error

Example Question #3 : Area Of A Parallelogram

A parallelogram has the base length of and the altitude of 2t-1 . Give the area of the parallelogram.

Possible Answers:

2t^2+t

2t^2-t

t^2+t

t^2

2t^2

Correct answer:

2t^2-t

Explanation:

The area of a parallelogram is given by:

Area=ba

Where is the base length and is the corresponding altitude. So we can write:

Area=t(2t-1)=2t^2-t

Report an Error

Example Question #4 : Area Of A Parallelogram

A parallelogram has a base length of which is 3 times longer than its corresponding altitude. The area of the parallelogram is 12 square inches. Give the .

Possible Answers:

$6\sqrt{3}$

$6\sqrt{2}$

Correct answer:

Explanation:

Base length is so the corresponding altitude is $\frac{t}{3}$ .

The area of a parallelogram is given by:

Area=ba

Where:

is the length of any base
is the corresponding altitude

So we can write:

$12=t\times \frac{t}{3}\Rightarrow t\times t=12\times 3\Rightarrow t^2=36\Rightarrow t=6$

$t\times t=12\times 3$

$t^{2}=36$

t=6

Report an Error

Example Question #4 : Area Of A Parallelogram

The length of the shorter diagonal of a rhombus is 40% that of the longer diagonal. The area of the rhombus is . Give the length of the longer diagonal in terms of .

Possible Answers:

$\frac{1}{5}\sqrt{K}$

$K\sqrt{\frac{5}{2}}$

$\sqrt{\frac{5K}{2}}$

$\sqrt{5K}$

$K\sqrt{\frac{2}{5}}$

Correct answer:

$\sqrt{5K}$

Explanation:

Let be the length of the longer diagonal. Then the shorter diagonal has length 40% of this. Since 40% is equal to $\frac{40}{100 } = \frac{40 \div 20 }{100 \div 20 } = \frac{2}{5}$ , 40% of is equal to $\frac{2}{5}D$ .

The area of a rhombus is half the product of the lengths of its diagonals, so we can set up, and solve for , in the equation:

$\frac{1}{2} \cdot \frac{2}{5}D \cdot D = K$

$\frac{1}{5}D^{2}= K$

$5\cdot \frac{1}{5}D^{2}=5\cdot K$

$D^{2}=5K$

$D =\sqrt{5K}$

Report an Error

Example Question #4 : Area Of A Parallelogram

The length of the shorter diagonal of a rhombus is two-thirds that of the longer diagonal. The area of the rhombus is square yards. Give the length of the longer diagonal, in inches, in terms of .

Possible Answers:

$\sqrt{ 3Q}$

$3\sqrt{ 3Q}$

$36\sqrt{ 3Q }$

$4\sqrt{ 3Q}$

$12\sqrt{ 3Q}$

Correct answer:

$36\sqrt{ 3Q }$

Explanation:

Let be the length of the longer diagonal in yards. Then the shorter diagonal has length two-thirds of this, or $\frac{2}{3}D$ .

The area of a rhombus is half the product of the lengths of its diagonals, so we can set up the following equation and solve for :

$\frac{1}{2} \cdot \frac{2}{3}D \cdot D = Q$

$\frac{1}{3}D ^{2} = Q$

$3\cdot \frac{1}{3}D ^{2} = 3 \cdot Q$

$D ^{2} = 3Q$

$D = \sqrt{3Q}$

To convert yards to inches, multiply by 36:

$\sqrt{ 3Q } \times 36 = 36\sqrt{ 3Q }$

Report an Error

Example Question #4 : Area Of A Parallelogram

The longer diagonal of a rhombus is 20% longer than the shorter diagonal; the rhombus has area . Give the length of the shorter diagonal in terms of .

Possible Answers:

$\sqrt{5N}$

$\sqrt{ \frac{N}{5}}$

$\sqrt{15N}$

$\sqrt{ \frac{5N}{3}}$

$\sqrt{ \frac{3N}{5}}$

Correct answer:

$\sqrt{ \frac{5N}{3}}$

Explanation:

Let be the length of the shorter diagonal. If the longer diagonal is 20% longer, then it measures 120% of the length of the shorter diagonal; this is

$\frac{120}{100} = \frac{120 \div 20}{100 \div 20} = \frac{6}{5}$

of , or $\frac{6}{5}D$ .

The area of a rhombus is half the product of the lengths of its diagonals, so we can set up an equation and solve for :

$\frac{1}{2} \cdot \frac{6}{5}D \cdot D = N$

$\frac{3}{5}D^{2} = N$

$\frac{5}{3} \cdot \frac{3}{5}D^{2} = \frac{5}{3} \cdot N$

$D^{2} = \frac{5N}{3}$

$D =\sqrt{ \frac{5N}{3}}$

Report an Error

Example Question #2 : Parallelograms

Find the area:

Question_5

Possible Answers:

$\small 12$

$\small 32$

$\small 16$

$\small 24$

Correct answer:

$\small 24$

Explanation:

The area of a parallelogram can be determined using the following equation:

$\small A=bh$

Therefore,

$\small A=8\times3=24$

Report an Error

Example Question #3 : Area Of A Parallelogram

Find the area of a parallelogram with a base of length 8 and a height of length 6.

Possible Answers:

A=48

A=24

A=28

A=36

A=7

Correct answer:

A=48

Explanation:

The area of a parallelogram is A=bh=(base)(height)

A=(6)(8)=48

Report an Error

View Pre-Algebra Tutors

Amelia
Certified Tutor

Austin College, Bachelor in Arts, Applied Mathematics. University of North Carolina at Charlotte, Master of Science, Applied ...

View Pre-Algebra Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View Pre-Algebra Tutors

Jeffrey
Certified Tutor

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in San Diego, LSAT Tutors in Miami, Calculus Tutors in Atlanta, Spanish Tutors in Houston, English Tutors in New York City, MCAT Tutors in Dallas Fort Worth, GRE Tutors in New York City, Statistics Tutors in Atlanta, Reading Tutors in Houston, Algebra Tutors in Boston

Popular Courses & Classes

MCAT Courses & Classes in Chicago, ISEE Courses & Classes in Philadelphia, GMAT Courses & Classes in Boston, LSAT Courses & Classes in Phoenix, GMAT Courses & Classes in Washington DC, GRE Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Miami, ISEE Courses & Classes in Miami, SSAT Courses & Classes in San Diego, Spanish Courses & Classes in Denver

Popular Test Prep

LSAT Test Prep in San Diego, GRE Test Prep in Phoenix, ISEE Test Prep in Philadelphia, SAT Test Prep in Denver, ACT Test Prep in Boston, SSAT Test Prep in Philadelphia, SSAT Test Prep in Washington DC, SSAT Test Prep in New York City, SSAT Test Prep in Miami, LSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Area of a Parallelogram

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #1 : Area Of A Parallelogram

Example Question #2 : Area Of A Parallelogram

Example Question #3 : Area Of A Parallelogram

Example Question #3 : Area Of A Parallelogram

Example Question #4 : Area Of A Parallelogram

Example Question #4 : Area Of A Parallelogram

Example Question #4 : Area Of A Parallelogram

Example Question #4 : Area Of A Parallelogram

Example Question #2 : Parallelograms

Example Question #3 : Area Of A Parallelogram

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: