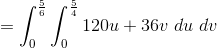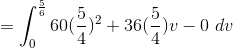We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Multivariable Calculus : Multivariable Calculus

Study concepts, example questions & explanations for Multivariable Calculus

Create An Account

All Multivariable Calculus Resources

14 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 Next →

Example Question #11 : Multivariable Calculus

Determine the length of the curve $\vec{r}(t)=\left \langle t,4\sin(2t),4\cos(2t)\right \rangle$ , on the interval $0\leq t\leq 2\pi$ .

Possible Answers:

$2\pi$

$2\pi\sqrt{65}$

$\pi$

$\sqrt{65}$

Correct answer:

$2\pi\sqrt{65}$

Explanation:

First we need to find the tangent vector, and find its magnitude.

$\vec{v}(t)=\vec{r}\ '(t)=\left \langle 1, 8\cos(2t), -8\sin(2t)\right \rangle$

$\left \| \vec{v}(t)\right \|=\sqrt{1^2+(8\cos(2t))^2+(-8\sin(2t))^2}$

$\left \| \vec{v}(t)\right \|=\sqrt{1+64\cos^2(2t)+64\sin^2(2t)}$

$\left \| \vec{v}(t)\right \|=\sqrt{1+64(\cos^2(2t)+\sin^2(2t))}$

$\left \| \vec{v}(t)\right \|=\sqrt{1+64}=\sqrt{65}$

Now we can set up our arc length integral

$L=\int_{a}^{b}\left \| \vec{v}(t)\right \|dt$

$L=\int_{0}^{2\pi} \sqrt{65}\ dt=t\sqrt{65}\Big|_{0}^{2\pi}=2\pi\sqrt{65}$

Report an Error

Example Question #12 : Multivariable Calculus

Convert the following into spherical coordinates.

$x=\sin(t)$

$y=\cos(t)$

z=1

Possible Answers:

$\rho=\sqrt{2}$

$\phi=0$

$\theta=\tan(\cot(t))$

$\rho=\sqrt{2}$

$\phi=\frac{\pi}{4}$

$\theta=\tan^{-1}(\cot(t))$

$\rho=2$

$\phi=-\frac{\pi}{4}$

$\theta=\tan^{-1}(\cot(t))$

$\rho=1$

$\phi=\frac{\pi}{2}$

$\theta=\tan(\cot(t))$

$\rho=\sqrt{2}$

$\phi=\frac{\pi}{4}$

$\theta=\tan^{-1}(\cot(t))$

Correct answer:

$\rho=\sqrt{2}$

$\phi=\frac{\pi}{4}$

$\theta=\tan^{-1}(\cot(t))$

Explanation:

In order to convert to spherical coordinates , we need to remember the conversion equations.

$\rho=\sqrt{x^2+y^2+z^2}$

$\theta=\tan^{-1}\Big(\frac{y}{x}\Big)$

$\phi=\tan^{-1}\Big(\frac{\sqrt{x^2+y^2}}{z}\Big)$

Now lets apply this to our problem.

$\rho=\sqrt{(\sin(t))^2+(\cos(t))^2+1^2}=\sqrt{1+1}=\sqrt{2}$

$\phi=\tan^{-1}\Big(\frac{\sqrt{(\sin{t})^2+(\cos{t})^2}}{1}\Big)=\tan^{-1}(1)=\frac{\pi}{4}$

$\theta=\tan^{-1}\Big(\frac{\cos(t)}{\sin(t)}\Big)=\tan^{-1}(\cot(t))$

Report an Error

Example Question #13 : Multivariable Calculus

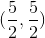
Evaluate $\int \int_R 3x+2y \ dA$ , where is the trapezoidal region with vertices given by (0,0) , (5,0) , $(\frac{5}{2}, \frac{5}{2})$ , and $(\frac{5}{2}, -\frac{5}{2})$ ,

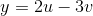
using the transformation x=2u+3v , and y=2u-3v .

Possible Answers:

$\frac{35}{4}$

$\frac{375}{4}$

$\frac{37}{4}$

$\frac{375}{2}$

Correct answer:

$\frac{375}{4}$

Explanation:

The first thing we have to do is figure out the general equations for the lines that create the trapezoid.

y=x

y=-x

y=-x+5

y=x-5

Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.

y=x

2u+3v=2u-3v

$-6v=0\rightarrow v=0$

y=-x

2u+3v=-2u+3v

$4u=0\rightarrow u=0$

y=-x+5

2u+3v=-2u+3v+5

$4u=5\rightarrow u=\frac{5}{4}$

y=x-5

2u+3v=2u-3v-5

$-6v=-5\rightarrow v=\frac{5}{6}$

So our region is a rectangle given by $0 \leq u \leq \frac{5}{4}$ , $0 \leq v \leq \frac{5}{6}$

Next we need to calculate the Jacobian.

$\begin{vmatrix} 2 & 3\\ 2 & -3 \end{vmatrix} =-6-6=-12$

Now we can put the integral together.

$\int_{0}^{\frac{5}{6}} \int_{0}^{\frac{5}{4}} (3(2u+3v)+2(2u-3v))) \cdot \left | -12\right | \ du\ dv$

$=\int_{0}^{\frac{5}{6}} \int_{0}^{\frac{5}{4}} 120u+36v \ du\ dv$

$=\int_{0}^{\frac{5}{6}} 60u^2+36uv \Big|_{0}^{\frac{5}{4}}\ dv$

$=\int_{0}^{\frac{5}{6}} 60( \frac{5}{4})^2+36(\frac{5}{4})v-0 \ dv$

$=\int_{0}^{\frac{5}{6}} \frac{375}{4}+45v \ dv$

$=\frac{375}{4}v+\frac{45}{2}v^2\Big|_{0}^{\frac{5}{6}} \ dv$

$=\frac{375}{4}\cdot\frac{5}{6}+\frac{45}{2}\cdot\Big(\frac{5}{6}\Big)^2 -0=\frac{375}{4}$

Report an Error

Example Question #14 : Multivariable Calculus

Convert the following into spherical coordinates.

$x=\sin(t)$

$y=\cos(t)$

z=1

Possible Answers:

$\rho=\sqrt{2}$
$\phi=0$
$\theta=\tan(\cot(t))$

$\rho=\sqrt{2}$
$\phi=\frac{\pi}{4}$
$\theta=\tan^{-1}(\cot(t))$

$\rho=\sqrt{2}$
$\phi=-\frac{\pi}{4}$
$\theta=\tan^{-1}(\cot(t))$

$\rho=2$
$\phi=-\frac{\pi}{4}$
$\theta=\tan^{-1}(\cot(t))$

$\rho=1$
$\phi=\frac{\pi}{2}$
$\theta=\tan(\cot(t))$

Correct answer:

$\rho=\sqrt{2}$
$\phi=\frac{\pi}{4}$
$\theta=\tan^{-1}(\cot(t))$

Explanation:

In order to convert to spherical coordinates , we need to remember the conversion equations.

$\rho=\sqrt{x^2+y^2+z^2}$

$\theta=\tan^{-1}\Big(\frac{y}{x}\Big)$

$\phi=\tan^{-1}\Big(\frac{\sqrt{x^2+y^2}}{z}\Big)$

Now lets apply this to our problem.

$\rho=\sqrt{(\sin(t))^2+(\cos(t))^2+1^2}=\sqrt{1+1}=\sqrt{2}$

$\phi=\tan^{-1}\Big(\frac{\sqrt{(\sin{t})^2+(\cos{t})^2}}{1}\Big)=\tan^{-1}(1)=\frac{\pi}{4}$

$\theta=\tan^{-1}\Big(\frac{\cos(t)}{\sin(t)}\Big)=\tan^{-1}(\cot(t))$

Report an Error

Example Question #1 : Divergence, Gradient, & Curl

Calculate the curl for the following vector field.

$\vec{F}=x^3y^2\ \vec{i}+x^2y^3z^4\ \vec{j}+x^2z^2\ \vec{k}$

Possible Answers:

$curl\ \vec{F}=\Big(4x^2y^3z^3\Big)\vec{i}+\Big(2xz^2\Big)\vec{j}+\Big(-2xy^3z^4+2x^3y\Big)\vec{k}$

$curl\ \vec{F}=\Big(2x^2z^3\Big)\vec{i}+\Big(2yz^2\Big)\vec{j}+\Big(-2x^3y\Big)\vec{k}$

$curl\ \vec{F}=0$

$curl\ \vec{F}=\Big(-4x^2y^3z^3\Big)\vec{i}+\Big(-2xz^2\Big)\vec{j}+\Big(2xy^3z^4-2x^3y\Big)\vec{k}$

$curl\ \vec{F}=\Big(2x^2z^3\Big)\vec{i}-\Big(2yz^2\Big)\vec{j}-\Big(-2x^3y\Big)\vec{k}$

Correct answer:

$curl\ \vec{F}=\Big(-4x^2y^3z^3\Big)\vec{i}+\Big(-2xz^2\Big)\vec{j}+\Big(2xy^3z^4-2x^3y\Big)\vec{k}$

Explanation:

In order to calculate the curl, we need to recall the formula.

$\\curl\ \vec{F}=\triangledown \times \vec{F}=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ \frac{\partial}{\partial x}& \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}\\ \\ \\ =\Big(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\ \Big)\vec{i}+\Big(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\ \Big)\vec{j}+\Big(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\ \Big)\vec{k}$

where , , and correspond to the components of a given vector field: $\vec{F}=P\vec{i}+Q\vec{j}+R\vec{k}$

Now lets apply this to out situation.

$curl\ \vec{F}=\triangledown \times \vec{F}=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\\\ \frac{\partial}{\partial x}& \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\\\ x^3y^2 & x^2y^3z^4 & x^2z^2 \end{vmatrix}$

$\\=\Big(\frac{\partial }{\partial y}\Big(x^2z^2\Big)-\frac{\partial}{\partial z}\Big(x^2y^3z^4\Big)\ \Big)\vec{i}+\Big(\frac{\partial}{\partial z}\Big(x^3y^2\Big)-\frac{\partial}{\partial x}\Big(x^2z^2\Big)\ \Big)\vec{j}+\Big(\frac{\partial}{\partial x}\Big(x^2y^3z^4\Big)-\frac{\partial}{\partial y}\Big(x^3y^2\Big)\ \Big)\vec{k}$

$=\Big(0-4x^2y^3z^3\Big)\vec{i}+\Big(0-2xz^2\Big)\vec{j}+\Big(2xy^3z^4-2x^3y\Big)\vec{k}$

Thus the curl is

$=\Big(-4x^2y^3z^3\Big)\vec{i}+\Big(-2xz^2\Big)\vec{j}+\Big(2xy^3z^4-2x^3y\Big)\vec{k}$

Report an Error

Example Question #2 : Divergence, Gradient, & Curl

Compute $div\vec{F}$ , where $\vec{F}=10x^2\ln(yz)\vec{i}+xyz\vec{j}+xz\ln(y)\vec{k}$ .

Possible Answers:

$div\vec{F}=20x\ln(yz)-xz-x\ln(y)$

$div\vec{F}=20x\ln(z)+yz+x\ln(y)$

$div\vec{F}=20x\ln(yz)+xz+x\ln(y)$

$div\vec{F}=20x\ln(yz)-xz+x\ln(y)$

$div\vec{F}=0$

Correct answer:

$div\vec{F}=20x\ln(yz)+xz+x\ln(y)$

Explanation:

All we need to do is calculate the partial derivatives and add them together.

$div\vec{F}=\frac{\partial}{\partial x}(10x^2\ln(yz))+\frac{\partial}{\partial y}(xyz)+\frac{\partial}{\partial z}(xz\ln(y))$

$div\vec{F}=20x\ln(yz)+xz+x\ln(y)$

Report an Error

Example Question #3 : Divergence, Gradient, & Curl

Calculate the curl for the following vector field.

$\vec{F}=x^3y^2\ \vec{i}+x^2y^3z^4\ \vec{j}+x^2z^2\ \vec{k}$

Possible Answers:

$curl\ \vec{F}=0$

$curl\ \vec{F}=\Big(2x^2z^3\Big)\vec{i}+\Big(2yz^2\Big)\vec{j}+\Big(-2x^3y\Big)\vec{k}$

$curl\ \vec{F}=\Big(2x^2z^3\Big)\vec{i}-\Big(2yz^2\Big)\vec{j}-\Big(-2x^3y\Big)\vec{k}$

$curl\ \vec{F}=\Big(4x^2y^3z^3\Big)\vec{i}+\Big(2xz^2\Big)\vec{j}+\Big(-2xy^3z^4+2x^3y\Big)\vec{k}$

$curl\ \vec{F}=\Big(-4x^2y^3z^3\Big)\vec{i}+\Big(-2xz^2\Big)\vec{j}+\Big(2xy^3z^4-2x^3y\Big)\vec{k}$

Correct answer:

$curl\ \vec{F}=\Big(-4x^2y^3z^3\Big)\vec{i}+\Big(-2xz^2\Big)\vec{j}+\Big(2xy^3z^4-2x^3y\Big)\vec{k}$

Explanation:

In order to calculate the curl, we need to recall the formula.

where , , and correspond to the components of a given vector field: $\vec{F}=P\vec{i}+Q\vec{j}+R\vec{k}$

Now lets apply this to out situation.

$=\Big(0-4x^2y^3z^3\Big)\vec{i}+\Big(0-2xz^2\Big)\vec{j}+\Big(2xy^3z^4-2x^3y\Big)\vec{k}$

Thus the curl is

$=\Big(-4x^2y^3z^3\Big)\vec{i}+\Big(-2xz^2\Big)\vec{j}+\Big(2xy^3z^4-2x^3y\Big)\vec{k}$

Report an Error

Example Question #4 : Divergence, Gradient, & Curl

Compute $div\vec{F}$ , where $\vec{F}=10x^2\ln(yz)\vec{i}+xyz\vec{j}+xz\ln(y)\vec{k}$ .

Possible Answers:

$div\vec{F}=20x\ln(yz)-xz+x\ln(y)$

$div\vec{F}=20x\ln(z)+yz+x\ln(y)$

$div\vec{F}=20x\ln(yz)-xz-x\ln(y)$

$div\vec{F}=0$

$div\vec{F}=20x\ln(yz)+xz+x\ln(y)$

Correct answer:

$div\vec{F}=20x\ln(yz)+xz+x\ln(y)$

Explanation:

All we need to do is calculate the partial derivatives and add them together.

$div\vec{F}=\frac{\partial}{\partial x}(10x^2\ln(yz))+\frac{\partial}{\partial y}(xyz)+\frac{\partial}{\partial z}(xz\ln(y))$

$div\vec{F}=20x\ln(yz)+xz+x\ln(y)$

Report an Error

Example Question #15 : Multivariable Calculus

Evaluate $\int \int \int_D y \ dV$ , where is the region below the plane z=x+1 , above the plane and between the cylinders x^2+y^2=1 , and x^2+y^2=9 .

Possible Answers:

$2 \pi$

$\frac{\pi}{2}$

$\pi$

$\frac{\pi}{4}$

Correct answer:

Explanation:

We need to figure out our boundaries for our integral.

We need to convert everything into cylindrical coordinates. Remeber we are above the plane, this means we are above z=0 .

$0\leq z \leq x+1 \rightarrow 0\leq z \leq r\cos(\theta)+1$

The region is between two circles x^2+y^2=1 , and x^2+y^2=9 .

This means that

$0 \leq \theta \leq 2\pi$

$1\leq r \leq 3$

$\int \int \int_D y \ dV=\int_{0}^{2\pi} \int_{1}^{3} \int_{0}^{r\cos(\theta)+1} r\sin(\theta) r\ dz \ dr \ d\theta$

$=\int_{0}^{2\pi} \int_{1}^{3} \int_{0}^{r\cos(\theta)+1} r^2\sin(\theta) \ dz \ dr \ d\theta$

$=\int_{0}^{2\pi} \int_{1}^{3} zr^2\sin(\theta) \Big|_{0}^{r\cos(\theta)+1} \ dr \ d\theta$

$=\int_{0}^{2\pi} \int_{1}^{3} (r\cos(\theta)+1)r^2\sin(\theta)-0 \ dr \ d\theta$

$=\int_{0}^{2\pi} \int_{1}^{3} r^3\sin(\theta)\cos(\theta)+r^2\sin(\theta) \ dr \ d\theta$

$=\int_{0}^{2\pi} \frac{1}{4}r^4\sin(\theta)\cos(\theta)+\frac{1}{3}r^3\sin(\theta) \Big|_{1}^{3}\ d\theta$

$=\int_{0}^{2\pi} (\frac{1}{4}(3)^4\sin(\theta)\cos(\theta)+\frac{1}{3}(3)^3\sin(\theta))-(\frac{1}{4}(1)^4\sin(\theta)\cos(\theta)+\frac{1}{3}(1)^3\sin(\theta)) \ d\theta$

$=\int_{0}^{2\pi} (\frac{81}{4}\sin(\theta)\cos(\theta)+9\sin(\theta))-(\frac{1}{4}\sin(\theta)\cos(\theta)+\frac{1}{3}\sin(\theta)) \ d\theta$

$=\int_{0}^{2\pi} 20\sin(\theta)\cos(\theta)+\frac{26}{3}\sin(\theta) \ d\theta$

$= -\frac{1}{2}\cdot20\cos^2(\theta)-\frac{26}{3}\cos(\theta)\Big|_{0}^{2\pi}$

$= -\frac{1}{2}\cdot20\cos^2(2\pi)-\frac{26}{3}\cos(2\pi)-(-\frac{1}{2}\cdot20\cos^2(0)-\frac{26}{3}\cos(0))$

$= -\frac{1}{2}\cdot20(1)-\frac{26}{3}(1)-(-\frac{1}{2}\cdot20(1)-\frac{26}{3}(1))$

$= -10-\frac{26}{3}-(-10-\frac{26}{3})=0$

Report an Error

Example Question #16 : Multivariable Calculus