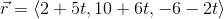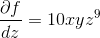All Multivariable Calculus Resources
Example Questions
Example Question #1 : Tangents & Normals
Find the equation of the tangent plane to 

First, we need to find the partial derivatives in respect to 





Remember that the general equation for a tangent plane is as follows:
Now lets apply this to our problem
Example Question #2 : Multivariable Calculus
Find the equation of the tangent plane to 

First, we need to find the partial derivatives in respect to 





Remember that the general equation for a tangent plane is as follows:
Now lets apply this to our problem
Example Question #1 : Dot & Cross Products
Let 

Find 
We are trying to find the cross product between 

Recall the formula for cross product.
If 


Now apply this to our situation.
Example Question #2 : Matrices & Vectors
Let 

Find 
We are trying to find the cross product between 

Recall the formula for cross product.
If 


Now apply this to our situation.
Example Question #1 : Matrices & Vectors
Write down the equation of the line in vector form that passes through the points 

Remember the general equation of a line in vector form:



Lets apply this to our problem.
Distribute the
Now we simply do vector addition to get
Example Question #1 : Vector Equations
Write down the equation of the line in vector form that passes through the points 

Remember the general equation of a line in vector form:



Lets apply this to our problem.
Distribute the
Now we simply do vector addition to get
Example Question #1 : Multivariable Calculus
Find 
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Example Question #2 : Multivariable Calculus
Find 
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Example Question #3 : Multivariable Calculus
Find 
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Example Question #3 : Partial Differentiation
Determine the length of the curve 

First we need to find the tangent vector, and find its magnitude.
Now we can set up our arc length integral
Certified Tutor
Certified Tutor
All Multivariable Calculus Resources