MCAT Physical : Newtonian Mechanics and Motion
Study concepts, example questions & explanations for MCAT Physical
All MCAT Physical Resources
Example Questions
Example Question #11 : Work, Energy, And Power
A 2kg box slides down a ramp a distance of two meters before it reaches the ground. The ramp has an angle of 
What is the work done on the box by friction?
Because the force of friction is parallel to the displacement of the box, we can solve for the work done by friction using the following equation.
Now, we need to define the force of friction or 
In this formula, 
Insert the value of acceleration due to gravity for 
Now, we can solve for the work done by friction.
Example Question #1 : Power
Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.
Over the course of the afternoon, they collide many times. Four collisions are described below.
Collision 1:
Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going 5m/s and subsequently slides into a stationary child 2. They remain linked together after the collision.
Collision 2:
Child 1 and child 2 are sliding in the same direction. Child 2, moving at 10m/s, slides into child 1, moving at 2m/s.
Collision 3:
The two children collide while traveling in opposite directions at 10m/s each.
Collision 4:
The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of +8m/s.
After child 1 comes to a full stop in the above collisions, she decides she wants to keep going. If she sits on a sled and moves across the lake surface by pushing off the lake surface with her feet, which scenario below will have her producing the most power? Assume the sled has a mass of 10kg.
She goes from 2m/s to 4m/s in 1s
She goes from 2m/s to 5m/s in 4s
She goes from 2m/s to 4m/s in 2s
She goes from 2m/s to 5m/s in 6s
She can't produce net power unless there is an external input of energy
She goes from 2m/s to 4m/s in 1s
Power is equal to work/time. The work that child 1 is performing is also equal to the change in kinetic energy. When she goes from 2m/s to 4m/s, she is increasing her kinetic energy by mv2.
This is the higest number of all the given scencarios. To arrive at this conclusion, you must compare calculations for the other given scenarios.
Example Question #11 : Work, Energy, And Power
A student holds a 10kg stack of books 1.5m above the ground for 20s. How much power was used to hold the books during this time?
15W
7.35W
0W
300W
147W
0W
Power is given by 
Example Question #82 : Mcat Physical Sciences
A 100-Watt lightbulb is 3m away from a window with height 0.5m and width 0.5m. At what rate does the bulb's energy exit the window? Assume the light spreads out evenly in all directions.
1.77J/s
2.65J/s
0.88J/s
8.33J/s
3.54J/s
0.88J/s
First we can find the intensity of light in Watts per square meter, when the light reaches the window, by using 
Assuming the light spreads out evenly in all directions, it has spread out over the area of a sphere of radius 3m by the time it reaches the window.
Multiplying this intensity times the area of the window gives the power (or energy per second) leaving the window.
Example Question #11 : Work, Energy, And Power
Which of the following CANNOT be a unit for power?
In physics, power is often given the unit, W, or watts. In mechanics, a watt often represents the amount of work done over a unit of time, or Joules per second.
In electrostatics a watt is expressed as the amount of current times the voltage, or as the current squared times the resistance.
A Newton-meter is a measure of energy or work, and can be written as a Joule, and is therefore the correct answer because it is not a measure of power.
Example Question #11 : Work, Energy, And Power
An elevator lifts 100kg a distance of ten meters in a time of four seconds. What is the power of the elevator?
The power of an elevator can be determined using the equation 
Example Question #17 : Work, Energy, And Power
Two students (student X and student Y) lift a boulder vertically from point A to point B. Student X directly lifts the boulder from point A to point B, whereas student Y uses a pulley to lift the boulder. This allows student Y to apply a force (
The vertical distance between point A and point B is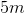 
The power exerted by student Y is __________.
equal to force exerted by student Y times two
equal to the power exerted by student X
equal to the force exerted by student Y times five
less than the power exerted by student X
less than the power exerted by student X
To answer this question you need to know the definitions of work and power:
The units of work and power are Joules and watts, respectively. The passage states that the amount of time it takes to complete the task is same for both students; therefore, you can ignore the effects of time on power.
The passage also states that student Y applies less force. Since student Y applies less force, he has to expend less energy (work) than student X. This means that student Y also has to exert less power. A reduction in force will reduce work, and subsequently reduce power. We can thus conclude that student Y exerts less power than student X.
Example Question #13 : Work, Energy, And Power
Two students (student X and student Y) lift a boulder vertically from point A to point B. Student X directly lifts the boulder from point A to point B, whereas student Y uses a pulley to lift the boulder. This allows student Y to apply a force (
The vertical distance between point A and point B is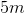
If student Y exerts a force of 
The first step is to find the force exerted by student X. The passage states that student Y exerts three times less force than student X; therefore, student X exerts three times more than student Y:
The second step is to find the amount of work done by student X.
Remember that student X directly lifts the boulder from point A to point B. This means that the distance the boulder travels is the vertical distance between point A and B (
The question states that time for the entire process is 
The correct answer is 
Example Question #1 : Kinetic Energy
A 5kg ball is attached to a 10m rope. The ball is held at a horizontal angle and allowed to fall freely with a pendulum-like motion. Assume there is no air resistance.
What is the velocity of the ball when it is at its lowest point?
This problem becomes much easier if we use the law of conservation of energy. Because there is no friction involved, all of the ball's potential energy was converted into kinetic energy when falling through the pendulum arc. As a result, the velocity at the bottom of the swing can be determined using the equation below.
Because the potential energy at the bottom of the swing is zero (relative to the starting point), and the velocity at the top is zero, we can simplify the equation.
Since the string is 10m long, we know that the lowest point will be 10m below the starting point.
Example Question #212 : Mcat Physical Sciences
Two children are playing with sleds on a snow-covered hill. Sam weighs 50kg, and his sled weighs 10kg. Sally weighs 40kg, and her sled weighs 12kg. When they arrive, they climb up the hill using boots. Halfway up the 50-meter hill, Sally slips and rolls back down to the bottom. Sam continues climbing, and eventually Sally joins him at the top.
They then decide to sled down the hill, but disagree about who will go first.
Scenario 1:
Sam goes down the hill first, claiming that he will reach a higher velocity. If Sally had gone first, Sam says they could collide.
Scenario 2:
Sally goes down the hill first, claiming that she will experience lower friction and thus reach a higher velocity. If Sam had gone first, Sally says they could collide.
Scenario 3:
Unable to agree, Sam and Sally tether themselves with a rope and go down together.
If the hill is frictionless, and after both Sally and Sam reach the bottom of the hill traveling at maximum velocity, who has lost more potential energy?
They have lost an equal amount of potential energy
Sally, because she is traveling faster
Sam, because his mass is larger
Sam, because he is traveling more slowly
Sally, because she experiences less friction
Sam, because his mass is larger
When they reach the bottom of the hill, Sam and Sally have both converted all of their potential energy into kinetic energy. We measured potential energy at 50m, so once they have lost 50m, the potential energy is 0, while the kinetic energy has reached maximum value. Because Sam has greater mass, he had more potential energy to convert to kinetic energy.
Certified Tutor
Certified Tutor
All MCAT Physical Resources
