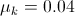We'll need to use the kinematic equation  to solve for d, the distance travelled when the book has stopped (). Before solving for d, we need to calculate the acceleration caused by the frictional force, by using the following steps.

1) Find the normal force on the book, .

2) Plug this normal force into  to solve for frictional force.

3) Find the acceleration caused by this frictional force, with .

Step 1 gives , so in step 2, , giving an acceleration of  to the left (which we will define to be the negative horizontal direction).

Returning to the original kinematic equation, .

Rearranging to solve for d gives 

Frictional force is given by the equation:

The only factors that can change frictional force are the coefficient of friction, which is determined by the materials of the surfaces in contact, and the normal force. Since the normal force must have a magnitude such that the sum of forces perpendicular to the table equals zero, both the mass of the book and any external vertical forces would influence the normal force, and thus also would influence the frictional force.

The coefficient of friction is a ratio of the force initiating horizontal displacement of an object and the downwards force of the object due to gravity

Note that the units cancel since we are finding the ratio of two forces. Although it is possible to have values for the coefficient of static friction greater than one, these systems are highly unusual.

The force of kinetic friction is given by the equation:

We can calculate the frictional force using the values from the question.

There are four force acting on the block: force from gravity, normal force, force of the spring scale, and force of friction. The normal force will be equal and opposite to the force of gravity, allowing us to cancel the forces in the vertical direction. This leaves us with a net force calculation for the horizontal force: the spring scale force and the force of friction. Note that the frictional force remains negative, as it acts in the opposite direction to the spring scale force.

Now that we know the net force and the mass of the block, we can calculate the acceleration using Newton's second law.

For formula for the force of friction is . We can rearrange this equation to solve for the coefficient of friction.

Remember that the normal force is equal to the force of gravity. Now we can plug in our given values and solve.

Don't forget to convert 500g to 0.5kg. The units cancel out, leaving the answer without any unit.

Since the box is moving when the net force on the box is determined, we can calculate the coefficient of kinetic friction for the box. The first step is determining what the net force on the box would be in the absence of friction. The net force on the box is given by the equation .

The difference between the frictionless net force and the net force with friction is 0.8N. This means that the force of kinetic friction on the box is 0.8N, acting opposite the direction of motion. Knowing this, we can solve for the coefficient of kinetic friction using the equation