All Linear Algebra Resources
Example Questions
Example Question #4 : Least Squares
Example Question #11 : Least Squares
Example Question #72 : Matrix Calculus
Example Question #71 : Matrix Calculus
Example Question #14 : Least Squares
It is recommended that you use a calculator with matrix arithmetic capability for this question.
Give the equation of the least squares regression line for the following data:




Round your coefficients to three decimal digits, if applicable.
Form the matrices 
using the abscissas and ordinates of the four points:

The least squares regression line is the line of the equation 
where 

This can be calculated as follows:
The least squares regression line is the line of the equation

Example Question #71 : Linear Algebra
Which of the following expressions is one for the gradient of the determinant of an 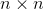

None of the other answers
The expression for the determinant of 
In order to find the gradient of the determinant, we take the partial derivative of the determinant expression with respect to some entry 

Example Question #71 : Linear Algebra
True or False, the Constrained Extremum Theorem only applies to skew-symmetric matrices.
False
True
False
It only applies to symmetric matrices, not skew-symmetric ones. The Constrained Extremum Theorem concerns the maximum and minimum values of the quadratic form 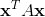

Example Question #1 : Eigenvalues As Optimization
The maximum value of a quadratic form 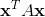



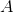
The eigenvalue with the greatest multiplicity
None of the other answers
The largest eigenvalue
The second largest eigenvalue
The smallest eigenvalue
The largest eigenvalue
This is the statement of the Constrained Extremum Theorem. Likewise, the minimum value of the quadratic form corresponds to the smallest eigenvalue of 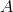
Example Question #1 : Operations And Properties
Which of the following matrices is a scalar multiple of the identity matrix?


The


For this problem we see that
And so

Example Question #1 : The Identity Matrix And Diagonal Matrices
Which of the following is true concerning diagonal matrices?
All of the other answers are false.
The zero matrix (of any size) is not a diagonal matrix.
The determinant of any diagonal matrix is 
The trace of any diagonal matrix is equal to its determinant.
The product of two diagonal matrices (in either order) is always another diagonal matrix.
The product of two diagonal matrices (in either order) is always another diagonal matrix.
You can verify this directly by proving it, or by multiplying a few examples on your calculator.
Certified Tutor
All Linear Algebra Resources

















































