ISEE Upper Level Quantitative : Hexagons
Study concepts, example questions & explanations for ISEE Upper Level Quantitative
All ISEE Upper Level Quantitative Resources
Example Questions
Example Question #91 : Geometry
Which is the greater quantity?
(a) The area of a regular hexagon with sidelength 1
(b) The area of an equilateral triangle with sidelength 2
(a) and (b) are equal
(b) is greater
It is impossible to tell from the information given
(a) is greater
(a) is greater
A regular hexagon with sidelength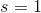 
Example Question #92 : Geometry
Which is the greater quantity?
(a) The perimeter of a regular pentagon with sidelength 1 foot
(b) The perimeter of a regular hexagon with sidelength 10 inches
It is impossible to tell from the information given.
(b) is greater.
(a) is greater.
(a) and (b) are equal.
(a) and (b) are equal.
The sides of a regular polygon are congruent, so in each case, multiply the sidelength by the number of sides to get the perimeter.
(a) Since one foot equals twelve inches, 
(b) Multiply: 
The two polygons have the same perimeter.
Example Question #93 : Geometry
A hexagon has six angles with measures
Which quantity is greater?
(a)
(b) 240
It is impossible to tell from the information given
(b) is greater
(a) is greater
(a) and (b) are equal
(a) and (b) are equal
The angles of a hexagon measure a total of 
The quantities are equal.
Example Question #96 : Isee Upper Level (Grades 9 12) Quantitative Reasoning
A hexagon has six angles with measures
Which quantity is greater?
(a)
(b)
It is impossible to tell from the information given.
(a) is greater.
(a) and (b) are equal.
(b) is greater.
(b) is greater.
The angles of a hexagon measure a total of
This makes (b) greater.
Example Question #97 : Isee Upper Level (Grades 9 12) Quantitative Reasoning
The angles of Hexagon A measure
The angles of Octagon B measure
Which is the greater quantity?
(A)
(B)
(B) is greater
It is impossible to determine which is greater from the information given
(A) is greater
(A) and (B) are equal
(B) is greater
The sum of the measures of a hexagon is 
The sum of the measures of an octagon is 
Example Question #98 : Isee Upper Level (Grades 9 12) Quantitative Reasoning
The angles of Pentagon A measure
The angles of Hexagon B measure
Which is the greater quantity?
(A)
(B)
(B) is greater
It is impossible to determine which is greater from the information given
(A) and (B) are equal
(A) is greater
(A) is greater
The sum of the measures of the angles of a pentagon is 
The sum of the measures of a hexagon is 
Example Question #7 : Hexagons
A regular hexagon has the same perimeter as the above right triangle. What is the length of one side of the hexagon?
The length cannot be determined from the information given.
By the Pythagorean Theorem, the hypotenuse of the right triangle is
The regular hexagon, which has six sides of equal length, has the same perimeter, so each side measures
Example Question #101 : Isee Upper Level (Grades 9 12) Quantitative Reasoning
A regular hexagon has the same perimeter as the above right triangle. What is the length of one side of the hexagon?
The length cannot be determined from the information given.
By the Pythagorean Theorem, the hypotenuse of the right triangle is
The regular hexagon, which has six sides of equal length, has the same perimeter, so each side measures
All ISEE Upper Level Quantitative Resources
