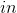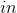Now, this could look like a difficult problem.  However, think of the equation for finding the length of the diagonal of a cube. It is like the Pythagorean Theorem, just adding an additional dimension:

(It is very easy, because the three lengths are all the same: ).

So, we know this, then:

To solve, you can factor out an  from the root on the right side of the equation:

Just by looking at this, you can tell that the answer is:

Now, use the equation for the volume of a cube:

(It is like doing the area of a square, then adding another dimension!).

For our data, it is:

We know that the volume of a cube can be found with the equation:

, where  is the side length of the cube.

Now, if the volume is , then we know:

Either with your calculator or with careful math, you can solve by taking the cube-root of both sides. This gives you:

This means that each side of the cube is   long; therefore, each face has an area of , or  . Since there are  sides to a cube, this means the total surface area is , or  .

This question is very easy. Do not over-think it! All you need to do is calculate the area of one side of the cube. Then, multiply that by  (since the cube has  sides). Each side of a cube is, of course, a square; therefore, the area of one side of this cube is , or  . This means that the whole cube has a surface area of  or  .

One of the faces of the cube could be drawn like this:

Notice that this makes a  triangle.

This means that we can create a proportion for the sides. On the standard triangle, the non-hypotenuse sides are both , and the hypotenuse is . This will allow us to make the proportion:

Multiplying both sides by , you get:

To find the area of the square, you need to square this value:

Now, since there are  sides to the cube, multiply this by  to get the total surface area:

It is easiest to think about diagonals like this by considering two points on a cube (if it were drawn in three dimensions).  We could draw it like this:

(Note that not all points are drawn in on the cube.)

The two points we are looking at are:

 and 

Solve this by using the distance formula.  This is very easy since one point is all s.  It is merely:

This is approximately .

It is easiest to think about diagonals like this by considering two points on a cube (if it were drawn in three dimensions). We could draw it like this:

(Note that not all points are drawn in on the cube.)

The two points we are looking at are:

 and 

Solve this by using the distance formula.  This is very easy since one point is all s.  It is merely:

This is approximately .

First, you need to find the side length of this cube. We know that the volume is:

, where  is the side length.

Therefore, based on our data, we can say:

Solving for  by taking the cube-root of both sides, we get:

Now, it is easiest to think about diagonals like this by considering two points on a cube (if it were drawn in three dimensions). We could draw it like this:

(Note that not all points are drawn in on the cube.)

The two points we are looking at are:

 and 

Solve this by using the distance formula. This is very easy since one point is all s. It is merely:

This is approximately .

First, you need to find the side length of this cube. We know that the surface area is defined by:

, where  is the side length. (This is because the cube is  sides of equal area).

Therefore, based on our data, we can say:

Take the square root of both sides and get:

Now, it is easiest to think about diagonals like this by considering two points on a cube (if it were drawn in three dimensions). We could draw it like this:

(Note that not all points are drawn in on the cube.)

The two points we are looking at are:

 and 

Solve this by using the distance formula. This is very easy since one point is all s. It is merely:

This is approximately .

We must begin by using the equation for the volume of a cube:

(It is like doing the area of a square, then adding another dimension!)

We know that the volume is .  Therefore, we can rewrite our equation:

Using your calculator, we can find the cube root of . It is . (If you get  just round up to . This is a calculator issue!).

This is the side length you need!

Another way you could do this is by cubing each of the possible answers to see which gives you a volume of .

Recall that the formula for the surface area of a cube is:

, where  is the length of a side of the cube.  This equation is easy to memorize because it is merely a multiplication of a single side () by  because a cube has  equal sides.

Now, we know that  is ; therefore, we can write:

Solve for :

Take the square root of both sides:

This is the length of one of your sides.