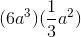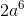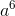Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : ISEE Upper Level (grades 9-12) Mathematics Achievement

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #111 : Numbers And Operations

Solve: $3^5 \cdot 3^{-8}$

Possible Answers:

$3^{13}$

$\frac{1}{3^{13}}$

$\frac{1}{9}$

$\frac{1}{27}$

Correct answer:

$\frac{1}{27}$

Explanation:

It is not necessary to evaluate both terms and multiply.

According to the rules of exponents, when we have the same bases raised to some power that are multiplied with each other, we can add the powers.

$3^5 \cdot 3^{-8} = 3^{5+( -8)} = 3^{-3}$

This term can be rewritten as a fraction.

$3^{-3 } = \frac{1}{3^3} = \frac{1}{27}$

The answer is: $\frac{1}{27}$

Report an Error

Example Question #551 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Which of the following is equivalent to the expression below?

$4^{x}\cdot2^{5}$

Possible Answers:

$8^{10x}$

$2^{2x+5}$

$8^{5x}$

$6^{5x}$

Correct answer:

$2^{2x+5}$

Explanation:

When exponents are multiplied by one another, and the base is the same, the exponents can be added together.

The first step is to try to create a common base.

$4^{x}\cdot2^{5}$

Given that the square of 2 is for, the expression can be rewritten as:

$2^{2}^{x}\cdot 2^{5}$

$2^{2x+5}$

Report an Error

Example Question #111 : Numbers And Operations

Simplify:

$(6a^3)(\frac{1}{3}a^2)$

Possible Answers:

a^6

a^5

2a^4

2a^5

2a^6

Correct answer:

2a^5

Explanation:

Based on the product rule for exponents in order to multiply two exponential terms with the same base, add their exponents:

$(x)^a(x)^b=x^{a+b}$

So we can write:

$(6a^3)\left(\frac{1}{3}a^2\right)=\left(\frac{6}{3}\right)\times a^{3+2}=2a^5$

Report an Error

Example Question #551 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Venn

Refer to the above Venn diagram.

Define universal set $U = \mathbb{N}$ , the set of natural numbers.

Define sets and as follows:

$A = \left \{ 1,5,9,13,17,21,... \right \}$

$B = \left \{ 2,5,8,11,14,17...\right \}$

Which of the following numbers is an element of the set represented by the gray area in the diagram?

Possible Answers:

101

105

103

102

104

Correct answer:

104

Explanation:

The gray area represents the set of all elements that are in but not in .

is the set of integers that, when divided by 3, yield remainder 2. Therefore, we can eliminate 102 and 105, both multiples of 3, and 103, which, when divided by 3, yields remainder 1.

is the set of integers that, when divided by 4, yield remainder 1. Since we do not want an element from this set, we can eliminate 101, but not 104.

104 is the correct choice.

Report an Error

Example Question #552 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Venn

In the above Venn diagram, the universal set is defined as $U = \left \{ a, b, c, d, e, f, g, h\right \}$ . Each of the eight letters is placed in its correct region.

What is $A \cap B$ ?

Possible Answers:

$A \cap B = \left \{ a,b,d,e,f,g,h \right \}$

$A \cap B = \left \{ a,c,f \right \}$

$A \cap B = \left \{ b,d,e,g,h \right \}$

$A \cap B = \left \{ a,f \right \}$

$A \cap B = \left \{ b,c,d,e,g,h \right \}$

Correct answer:

$A \cap B = \left \{ a,f \right \}$

Explanation:

$A \cap B$ is the intersection of sets and - that is, the set of all elements of that are elements of both and . We want all of the letters that fall in both circles, which from the diagram can be seen to be and . Therefore,

$A \cap B = \left \{ a,f \right \}$

Report an Error

Example Question #553 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Venn

In the above Venn diagram, the universal set is defined as $U = \left \{ a, b, c, d, e, f, g, h\right \}$ . Each of the eight letters is placed in its correct region. Which of the following is equal to $\overline{A\cap B}$ ?

Possible Answers:

$\overline{A\cap B} = \left \{ a,f\right \}$

$\overline{A\cap B} = \left \{ c\right \}$

$\overline{A\cap B} = \left \{ b,d,e,g,h\right \}$

$\overline{A\cap B} = \left \{ a,c,f\right \}$

$\overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}$

Correct answer:

$\overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}$

Explanation:

$\overline{A \cap B}$ is the complement of $A \cap B$ - the set of all elements in not in $A \cap B$ .

$A \cap B$ is the intersection of sets and - that is, the set of all elements of that are elements of both and . Therefore, $\overline{A \cap B}$ is the set of all elements that are not in both and , which can be seen from the diagram to be all elements except and . Therefore,

$\overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}$ .

Report an Error

Example Question #4 : Data Analysis And Probability

Venn

Possible Answers:

$\overline{A\cup B} = \left \{ b,c,d,e,g,h\right \}$

$\overline{A\cup B} = \left \{ b,d,e,g,h\right \}$

$\overline{A\cup B} = \left \{ c\right \}$

$\overline{A\cup B} = \left \{ a,c,f\right \}$

$\overline{A\cup B} = \left \{ a,f\right \}$

Correct answer:

$\overline{A\cup B} = \left \{ c\right \}$

Explanation:

$\overline{A\cup B}$ is the complement of $A\cup B$ - the set of all elements in not in $A\cup B$ .

$A\cup B$ is the union of sets and - the set of all elements in either or . Therefore, $\overline{A\cup B}$ is the set of all elements in neither nor , which can be seen from the diagram to be only one element - . Therefore,

$\overline{A\cup B} = \left \{ c\right \}$

Report an Error

Example Question #554 : Isee Upper Level (Grades 9 12) Mathematics Achievement

The following Venn diagram depicts the number of students who play hockey, football, and baseball. How many students play football and baseball?

Problem_9

Possible Answers:

Correct answer:

Explanation:

The number of students who play football or baseball can by finding the summer of the number of students who play football alone, baseball alone, baseball and football, and all three sports.

30+20+3+3=56

Report an Error

Example Question #1 : Data Analysis And Probability

A class of students was asked whether they have cats, dogs, or both.The results are depicted in the following Venn diagram. How many students do not have a dog?

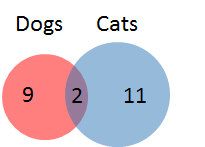
Question_5

Possible Answers:

Correct answer:

Explanation:

First, calculate the number of students with a dog:
9+2=11

Next, subtract the number of students with a dog from the total number of students.

30-11=19

Report an Error

Example Question #1 : How To Find The Answer From A Table

If a standard die is rolled, what is the probability of getting a 1 or a 2?

Possible Answers:

$\dpi{100} \frac{1}{3}$

$\dpi{100} 2$

$\dpi{100} \frac{1}{2}$

$\dpi{100} \frac{1}{6}$

Correct answer:

$\dpi{100} \frac{1}{3}$

Explanation:

We need to know the total number of possibilities, and the total number of ways to achieve our goal.

A standard die has 6 faces, so there are a total of 6 numbers that we could roll.

We want to roll a 1 or a 2, which means there are 2 ways that we can succeed (rolling a 1 or a 2).

Thus, we have a probability of success as $\dpi{100} \frac{2}{6}$ which reduces to $\dpi{100} \frac{1}{3}$ .

Report an Error

View Tutors

Claire
Certified Tutor

Augustana College, Bachelor of Fine Arts, Music Teacher Education.

View Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

View Tutors

Ana
Certified Tutor

Grand Canyon University, Bachelors, Education. Grand Canyon University, Masters, Education.

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Philadelphia, Spanish Tutors in Miami, Reading Tutors in Philadelphia, Physics Tutors in Phoenix, GRE Tutors in Miami, Spanish Tutors in Los Angeles, GRE Tutors in San Francisco-Bay Area, French Tutors in Chicago, Calculus Tutors in Miami, Biology Tutors in San Francisco-Bay Area

Popular Courses & Classes

Spanish Courses & Classes in Phoenix, ISEE Courses & Classes in Philadelphia, MCAT Courses & Classes in Phoenix, LSAT Courses & Classes in Boston, MCAT Courses & Classes in Miami, SAT Courses & Classes in Houston, ISEE Courses & Classes in Washington DC, SSAT Courses & Classes in Boston, ACT Courses & Classes in Los Angeles, LSAT Courses & Classes in Philadelphia

Popular Test Prep

GRE Test Prep in Chicago, SAT Test Prep in San Diego, ACT Test Prep in Los Angeles, SAT Test Prep in Miami, ISEE Test Prep in New York City, SAT Test Prep in Philadelphia, SAT Test Prep in Chicago, ACT Test Prep in Dallas Fort Worth, SAT Test Prep in Boston, SSAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : ISEE Upper Level (grades 9-12) Mathematics Achievement

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #111 : Numbers And Operations

Example Question #551 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #111 : Numbers And Operations

Example Question #551 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #552 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #553 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #4 : Data Analysis And Probability

Example Question #554 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #1 : Data Analysis And Probability

Example Question #1 : How To Find The Answer From A Table

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: