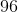Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : ISEE Upper Level (grades 9-12) Mathematics Achievement

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #431 : Geometry

You have a tennis ball canister which is cylindrical. If the radius of the cylinder is 3.5 cm, and the height is 21 cm, what is the volume of the canister?

Possible Answers:

$V=257.25 \pi cm^3$

$V=25.725 \pi cm^3$

V=257.25 cm^3

$V=73.5 \pi cm^3$

Correct answer:

$V=257.25 \pi cm^3$

Explanation:

You have a tennis ball canister which is cylindrical. If the radius of the cylinder is 3.5 cm, and the height is 21 cm, what is the volume of the canister?

Begin with the formula for volume of a cylinder:

$V=\pi r^2 h$

Where r is our radius and h is our height.

Note that the formula is just the formula for the area of a circle times the height, because a cylinder is really just a circle with height.

Now, plug in what we know and solve for V

$V=\pi (3.5cm)^2 (21cm)=\pi(12.25cm*21cm)=257.25 \pi cm^3$

So our answer is:

$V=257.25 \pi cm^3$

Report an Error

Example Question #431 : Isee Upper Level (Grades 9 12) Mathematics Achievement

A cylinder has the following measurements:

Height: 6in
Diameter: 16in

Find the volume.

Possible Answers:

$288\pi \text{ in}^3$

$48\pi \text{ in}^3$

$384\pi \text{ in}^3$

$576\pi \text{ in}^3$

$96\pi \text{ in}^3$

Correct answer:

$384\pi \text{ in}^3$

Explanation:

To find the volume of a cylinder, we will use the following formula:

$V = \pi r^2 h$

where r is the radius and h is the height of the cylinder.

Now, we know the diameter of the cylinder is 16in. We also know the diameter is two times the radius. Therefore, the radius is 8in.

We also know the height of the cylinder is 6in.

Knowing all of this, we can substitute into the formula. We get

$V = \pi \cdot(8\text{in})^2 \cdot 6\text{in}$

$V = \pi \cdot 64\text{in}^2 \cdot 6\text{in}$

$V = \pi \cdot 384\text{in}^3$

$V = 384\pi \text{ in}^3$

Report an Error

Example Question #112 : Solid Geometry

A cylinder has the following measurements:

Height: 12in
Diameter: 10in

Find the volume.

Possible Answers:

$300\pi \text{ in}^3$

$720\pi \text{ in}^3$

$360\pi \text{ in}^3$

$576\pi \text{ in}^3$

$120\pi \text{ in}^3$

Correct answer:

$300\pi \text{ in}^3$

Explanation:

To find the volume of a cylinder, we will use the following formula:

$V = \pi \cdot r^2 \cdot h$

where r is the radius, and h is the height of the cylinder.

Now, we know the diameter of the cylinder is 10in. We also know the diameter is two times the radius. Therefore, the radius is 5in.

We know the height of the cylinder is 12in.

Knowing all of this, we can substitute into the formula. We get

$V = \pi \cdot (5\text{in})^2 \cdot 12\text{in}$

$V = \pi \cdot 25\text{in}^2 \cdot 12\text{in}$

$V = \pi \cdot 300\text{in}^3$

Report an Error

Example Question #113 : Solid Geometry

Find the volume of a cylinder with a height of 9in and a radius of 8in.

Possible Answers:

$324\pi \text{ in}^3$

$648\pi \text{ in}^3$

$144\pi \text{ in}^3$

$576\pi \text{ in}^3$

$212\pi \text{ in}^3$

Correct answer:

$576\pi \text{ in}^3$

Explanation:

To find the volume of a cylinder, we will use the following formula:

$V = \pi r^2 h$

where r is the radius and h is the height of the cylinder.

Now, we know the radius of the cylinder is 8in and the height of the cylinder is 9in.

So, we get

$V = \pi \cdot (8\text{in})^2 \cdot 9\text{in}$

$V = \pi \cdot 64\text{in}^2 \cdot 9\text{in}$

$V = \pi \cdot 576\text{in}^3$

$V = 576\pi \text{ in}^3$

Report an Error

Example Question #431 : Isee Upper Level (Grades 9 12) Mathematics Achievement

For a cylinder, if the radius of the base is 4, and the height is 10, what is the volume?

Possible Answers:

$40\pi$

$160 \pi$

$80\pi$

$84\pi$

$48\pi$

Correct answer:

$160 \pi$

Explanation:

Write the formula to find the volume of a cylinder.

$V = \pi r^2h$

Substitute the known dimensions.

$V = \pi (4^2)(10)$

Solve for the volume.

$V =160 \pi$

The answer is: $160 \pi$

Report an Error

Example Question #432 : Isee Upper Level (Grades 9 12) Mathematics Achievement

If a cylinder has a height of 6 mm and a radius of 12 mm, what is its surface area?

Possible Answers:

432 mm

$144 \pi mm^2$

$288 \pi mm^2$

$432 \pi mm^2$

Correct answer:

$432 \pi mm^2$

Explanation:

If a cylinder has a height of 6 mm and a radius of 12 mm, what is its surface area?

Find surface area with the following formula:

$A=2\pi r h +2\pi r^2$

This works because we are adding the area of the two bases to the area of the side.

Plug in and simplify:

$A=2\pi (12mm)(6mm) +2\pi (12mm)^2=144\pi mm^2+288\pi mm^2=432 \pi mm^2$

Report an Error

Example Question #431 : Geometry

Find the volume of a cylinder with a diameter of 14cm and a height of 8cm.

Possible Answers:

$56\pi \text{ cm}^3$

$896\pi \text{ cm}^3$

$976\pi \text{ cm}^3$

$112\pi \text{ cm}^3$

$392\pi \text{ cm}^3$

Correct answer:

$392\pi \text{ cm}^3$

Explanation:

To find the volume of a cylinder, we will use the following formula:

$V = \pi r^2 h$

where r is the radius and h is the height of the cylinder.

Now, we know the diameter of the cylinder is 14cm. We also know that the diameter is two times the radius. Therefore, the radius is 7cm.

We know the height of the cylinder is 8cm.

Knowing all of this, we can substitute into the formula. We get

$V = \pi \cdot (7\text{cm})^2 \cdot 8\text{cm}$

$V = \pi \cdot 49\text{cm}^2 \cdot 8\text{cm}$

$V = \pi \cdot 392\text{cm}^3$

$V = 392\pi \text{ cm}^3$

Report an Error

Example Question #433 : Isee Upper Level (Grades 9 12) Mathematics Achievement

What is the greatest common factor of 72 and 80?

Possible Answers:

Correct answer:

Explanation:

Find the factors of 72 and 80; the greatest common factor is the greatest number in both lists.

$72: 1,2,3,4,6,\underline{8},9,12,18,24,36,72$

$80:1,2,4,5,\underline{8},10,16,20,40,80$

$\textrm{GCF}(72,80) = 8$

Report an Error

Example Question #434 : Isee Upper Level (Grades 9 12) Mathematics Achievement

What is the greatest common factor of 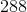288 and 528 ?

Possible Answers:

Correct answer:

Explanation:

Fully factor 288 and 528 . Circle the factors in common:

Problem_6

Multiple the common factors to find the greatest common factor:

$GCF=2\times2\times2\times2\times3=48$

Report an Error

Example Question #3 : How To Find The Greatest Common Factor

Which of these numbers is relatively prime with 10?

Possible Answers:

Correct answer:

Explanation:

We are looking for a number that shares no factors with 10 other than 1. 20 and 28 can be eliminated since 2 divides 10, 20, 28. 25 and 35 can be eliminated since 5 divides 10, 25, and 25.

21 is the correct choice; $10 = 2\times 5$ and $21 = 3 \times 7$ . Since they share no prime factors, GCF (10,21) = 1 , and 10 and 21 are relatively prime.

Report an Error

View Tutors

Lazaro
Certified Tutor

Miami Dade College, Bachelor of Engineering, Computer Hardware Engineering.

View Tutors

Chase
Certified Tutor

Western Governors University, Bachelor of Science, Mathematics.

View Tutors

Ericka
Certified Tutor

Southern Nazarene University, Bachelors, Network Engineering and Management . Oklahoma State University-Main Campus, Master o...

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Seattle, Calculus Tutors in Phoenix, Biology Tutors in Phoenix, Algebra Tutors in Seattle, ACT Tutors in New York City, ISEE Tutors in Miami, Computer Science Tutors in Philadelphia, SAT Tutors in Philadelphia, Spanish Tutors in Seattle, GRE Tutors in Denver

Popular Courses & Classes

ACT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in New York City, LSAT Courses & Classes in Washington DC, SAT Courses & Classes in New York City, Spanish Courses & Classes in Denver, GMAT Courses & Classes in Atlanta, GRE Courses & Classes in Atlanta, Spanish Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Houston, MCAT Courses & Classes in San Diego

Popular Test Prep

SAT Test Prep in Boston, ACT Test Prep in Phoenix, LSAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Denver, LSAT Test Prep in Chicago, SAT Test Prep in Washington DC, MCAT Test Prep in Chicago, LSAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Denver, SSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : ISEE Upper Level (grades 9-12) Mathematics Achievement

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #431 : Geometry

Example Question #431 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #112 : Solid Geometry

Example Question #113 : Solid Geometry

Example Question #431 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #432 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #431 : Geometry

Example Question #433 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #434 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #3 : How To Find The Greatest Common Factor

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: