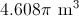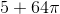All ISEE Upper Level Math Resources
Example Questions
Example Question #421 : Geometry
Find the volume of a cone with a base diameter of 2, and a height of 10.
Write the formula to find the volume of a cone.
The diameter is 2, which means the radius is 1. Substitute the known dimensions.
The answer is:
Example Question #182 : Geometry
A cone has height 240 centimeters; its base has radius 80 centimeters. Give its volume in cubic meters.
Convert both dimensions from centimeters to meters by dividing by 100:
Height: 240 centimeters = 
Radius: 80 centimeters = 
Substitute 
Example Question #1 : How To Find The Surface Area Of A Cone
What is the surface area of a cone with the following measurements?
The surface area of a cone can be found with the following equation:
Example Question #1 : Cylinders
The axle for a toy car has a length of 4 inches and a diameter of a quarter inch. What is the volume of the axle? Assume it is a cylinder.
The axle for a toy car has a length of 4 inches and a diameter of a quarter inch. What is the volume of the axle? Assume it is a cylinder.
Use the following formula for volume of a cylinder
Where r and h are our radius and height, respectively.
In this case, we first need to change our diameter to radius. Because our diameter is one quarter of an inch, our radius will be one eighth of an inch.
Plug it in to get:
Simplify to get:
Example Question #2 : How To Find The Volume Of A Cylinder
You are visiting the drive-through at the bank. You put you money in a cylindrical tube with a height of 8 inches and a radius of 2 inches. What is the volume of the tube?
Not enough information
You are visiting the drive-through at the bank. You put you money in a cylindrical tube with a height of 8 inches and a radius of 2 inches. What is the volume of the tube?
Begin with the formula for volume of a cylinder:
We have r and h, which are our radius and height, respectively. Plug them in and solve
Making our answer:
Example Question #3 : How To Find The Volume Of A Cylinder
Find the volume of a cylinder with the following measurements:
- diameter = 8cm
- height = 5cm
To find the volume of a cylinder, we will use the following formula:
where r is the radius and h is the height of the cylinder.
Now, we know the diameter of the cylinder is 8cm. We know that the diameter is two times the radius. Therefore, the radius is 4cm.
We also know the height of the cylinder is 5cm.
Knowing this, we can substitute into the formula.
Example Question #4 : How To Find The Volume Of A Cylinder
Find the volume of a cylinder with a diameter of 8in and a height of 7in.
To find the volume of a cylinder, we will use the following formula:
where r is the radius and h is the height of the cylinder.
Now, we know the diameter of the cylinder is 8in. We also know the diameter is two times the radius. Therefore, the radius is 4in.
We also know the height of the cylinder is 7in.
Knowing all of this, we can substitute into the formula. We get
Example Question #5 : How To Find The Volume Of A Cylinder
Find the volume of a cylinder with a diameter of 14in and a height of 12in.
To find the volume of a cylinder, we will use the following formula:
where r is the radius, and h is the height of the cylinder.
Now, we know the diameter of the cylinder is 14in. We also know the diameter is two times the radius. Therefore, the radius is 7in.
We know the height of the cylinder is 12in.
Knowing all of this, we can substitute into the formula. We get
Example Question #6 : How To Find The Volume Of A Cylinder
Your family owns a farm with a silo for storing grain. If the silo is 40 feet tall and 15 feet in diameter, what volume of grain can it hold?
Your family owns a farm with a silo for storing grain. If the silo is 40 feet tall and 15 feet in diameter, what volume of grain can it hold?
Begin with the formula for volume of a cylinder.
A cylinder is just a circle with height.
So, we know the height is 40 ft, but what is r?
If you said 15, you would be on track to get the problem wrong. That is because the diameter is 15 ft, so our radius is only 7.5 ft.
Plug these in to get our answer:
Our answer should be
Example Question #7 : How To Find The Volume Of A Cylinder
Let
Find the volume of a cylinder with a diameter of 12cm and a height of 7cm.
To find the volume of a cylinder, we will use the following formula:
where r is the radius and h is the height of the cylinder.
Now, we know the diameter is 12cm. We know that the diameter is two times the radius. Therefore, the radius is 6cm.
We know the height of the cylinder is 7cm.
We know that 
Knowing all of this, we can substitute into the formula. We get
All ISEE Upper Level Math Resources