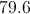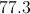ISEE Middle Level Quantitative : ISEE Middle Level (grades 7-8) Quantitative Reasoning
Study concepts, example questions & explanations for ISEE Middle Level Quantitative
All ISEE Middle Level Quantitative Resources
Example Questions
Example Question #3 : How To Find Mean
The six students in the science club weigh 145 pounds, 172 pounds, 166 pounds, 159 pounds, 153 pounds, and 201 pounds. Find the mean of their weights.
Add the weights, then divide the sum by six:
Example Question #3 : Mean
Give the mean of the data set
There are six elements, so to find the mean, add the elements and divide by six:
Example Question #281 : Isee Middle Level (Grades 7 8) Quantitative Reasoning
The mean of the weights of the eleven students in the math club is 186 pounds. Which is the greater quantity?
(A) The sum of the weights of the students
(B) One ton
(B) is greater
(A) is greater
(A) and (B) are equal
It is impossible to determine which is greater from the information given
(A) is greater
One ton is equal to 2,000 pounds.
The mean of the weights of the students is the total of their weights divided by the number of students.
Let 
(A) is greater.
Example Question #281 : Isee Middle Level (Grades 7 8) Quantitative Reasoning
David scored 77, 92, and 80 on his first 3 tests. He currently has a test score average of 83. What grade would David need on the next test to increase his test score average to 85?
You can find the average of a set of numbers by adding up the numbers and dividing by how many numbers are in the data set. Since David is trying to acheive an average of 85 by his fourth test, we should multiply 85 by 4.
The result is the number that the four tests should total in order to achieve an average of 85. Then, add up the test scores Daid has recieved so far:
If you subtract this number (the total from the test scores so far) from 340, the result will be the score needed to achieve the 85 average.
David must score a 91 on his fourth test.
Example Question #4 : How To Find Mean
June ran 2 miles Monday, 3 miles Tuesday, 3 miles Thursday, and 2 miles Friday. How many miles did June run on average from Monday to Friday?
You can find the average of a set of numbers by adding up all the numbers in that set and dividing by how many numbers you added total. Here is a summary of our set:
Monday: 2 miles
Tuesday: 3 miles
Wednesday: 0 miles
Thursday: 3 miles
Friday: 2 miles
Keep in mind that we are looking for the average number of miles June ran Monday through Friday, and that there are 5 days in that period. You must also account for the 0 miles that June ran on Wednesday.
June ran a total of 10 miles during that 5 day period. You must then divide by the number of days in order to get the average.
Example Question #1 : How To Find Mean
In a group of 4 books, the average number of pages is is 10. Juan adds a book with 20 pages to the group. What is the new average number of pages?
If the average of 4 books was 10, then the total number of pages was 
Example Question #2 : How To Find Mean
Give the mean of the data set (nearest tenth, if applicable):
Add the six elements and divide the sum by 6:
Example Question #1 : How To Find Mean
Find the mean of this set of numbers:
54, 41, 99, 120, 66.
Firrst, add the numbers:
Then, divide by the amount of numbers in the set:
Answer: The mean is 76.
Example Question #3 : How To Find Mean
Give the mean of the following eight scores:
Divide the sum of the scores by eight:
Example Question #3 : How To Find Mean
Give the mean of the following nine scores:
Divide the sum of the scores by nine:
Certified Tutor
Certified Tutor
All ISEE Middle Level Quantitative Resources
