Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Middle Level Math : Geometry

Study concepts, example questions & explanations for ISEE Middle Level Math

Create An Account

All ISEE Middle Level Math Resources

6 Diagnostic Tests 303 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : How To Find The Perimeter Of A Parallelogram

If a parallelogram has side lengths of and , what is the perimeter?

Possible Answers:

Correct answer:

Explanation:

The perimeter of a parallelogram is two times the two side lengths and add them together.

$\\P=s_1+s_2+s_3+s_4 \\s_1=s_3 \\s_2=s_4 \\P=s_a+s_a+s_b+s_b \\P=2s_a+2s_b$

Therefore, this particular problem becomes as follows.

2*7=14

and

2*3=6

14+6=20 .

Report an Error

Example Question #1303 : Concepts

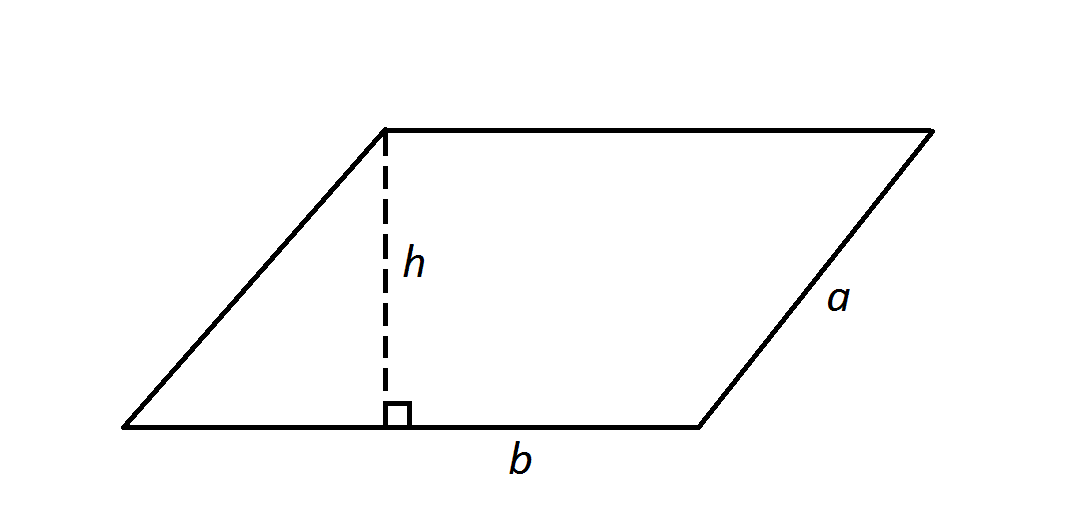
Parallelogram

Note: Figure NOT drawn to scale.

$a = 18\; \textrm{in} ,b=26\; \textrm{in},h=12\; \textrm{in}$ , where and represent side lengths of the parallelogram and represents the height.

Find the perimeter of the parallelogram in the diagram.

Possible Answers:

$88 \;\textup{in}$

$76 \;\textup{in}$

$44 \;\textup{in}$

$60 \;\textup{in}$

$46 \;\textup{in}$

Correct answer:

$88 \;\textup{in}$

Explanation:

The perimeter of the parallelogram is the sum of the four side lengths - here, that formula becomes

P = a + b + a + b = 18 + 26 + 18 + 26 = 88 .

Note that the height is irrelevant to the answer.

Report an Error

Example Question #1 : Parallelograms

Find the area of the following parallelogram:

Note: The formula for the area of a parallelogram is $A=b\times h$ .

Possible Answers:

$50\: in^2$

$30\: in^2$

$60\: in^2$

$32\: in^2$

Correct answer:

$50\: in^2$

Explanation:

The base of the parallelogram is 10, while the height is 5.

$A=b\times h$

$A=10\times5=50\: in^2$

Report an Error

Example Question #1 : How To Find The Area Of A Parallelogram

Find the area:

Question_5

Possible Answers:

$\small 12$

$\small 32$

$\small 16$

$\small 24$

Correct answer:

$\small 24$

Explanation:

The area of a parallelogram can be determined using the following equation:

$\small A=bh$

Therefore,

$\small A=8\times3=24$

Report an Error

Example Question #1 : How To Find The Area Of A Parallelogram

You can solve the area of a parallelogram when you know the lengths of each of the sides. True or False?

Possible Answers:

TRUE

FALSE

Correct answer:

FALSE

Explanation:

The area of a parallelogram is found by computing base * height . In this situation, you would have the base which is the bottom side but you would not have the height measurement. Since you would not be able to solve for the area with just the side lengths, the statement is FALSE .

Report an Error

Example Question #2 : How To Find The Area Of A Parallelogram

If a parallelogram has side lengths of and , what is the area?

Possible Answers:

Cannot be determined.

Correct answer:

Cannot be determined.

Explanation:

To find the area of a parallelogram, you use the formula,

A=base*height .

Since the height in this problem is not known, you cannot solve for area.

Report an Error

Example Question #3 : How To Find The Area Of A Parallelogram

Find the area of a parallelogram with a base of 6 inches and a height of 9 inches.

Possible Answers:

$27\text{in}$

$54\text{in}^2$

$27\text{in}^2$

$54\text{in}$

$30\text{in}^2$

Correct answer:

$54\text{in}^2$

Explanation:

To find the area of a parallelogram, we will use the following formula:

$\text{area of a parallelogram} = b \cdot h$

where b is the base and h is the height of the parallelogram.

Now, we know the base has a length of 6 inches. We also know it has a height of 9 inches. Knowing this, we can substitute into the formula. We get

$\text{area of a parallelogram} = 6\text{in} \cdot 9\text{in}$

$\text{area of a parallelogram} = 54\text{in}^2$

Report an Error

Example Question #2 : Parallelograms

Find the area of the parallelogram with a base length of 6 and a height of 15.

Possible Answers:

Correct answer:

Explanation:

Write the area formula of a parallelogram.

A=bh

Substitute the dimensions into the formula.

A=6(15) = 90

The answer is:

Report an Error

Example Question #1 : How To Find A Square On A Coordinate Plane

Which of the following is a vertex of the square?

Question_12

Possible Answers:

$\small (-2,1)$

$\small (-1,-4)$

$\small (-1,2)$

$\small (2,4)$

$\small (1,-4)$

Correct answer:

$\small (-1,2)$

Explanation:

The coordinates of a point are determined by the distance from the origin. The first point in the ordered pair is the number of units to the left or right of the origin. Negative numbers indicate the number of units to the left while positive numbers indicate the number of units to the right. The second number indicates the number of units above or below the origin. Positive numbers indicate the number of units above while negative numbrs indicate the number of units below the origin. The vertices of the square are:
$\small (-1,2); (-1,4); (1,2); (-1,4)$

Report an Error

Example Question #1 : How To Find The Points On A Coordinate Plane

Which of the following points will you find on the -axis?

Possible Answers:

(-30,30)

(30,30)

(0,-30)

(30, 0)

(30,-30)

Correct answer:

(0,-30)

Explanation:

A point is located on the -axis if and only if it has -coordinate (first coordinate) 0. Of the five choices, only (0,-30) fits that description.

Report an Error

View Tutors

Yongmao
Certified Tutor

Nankai University, Bachelor of Science, Chemistry. Washington University in St Louis, Doctor of Philosophy, Organic Chemistry.

View Tutors

Sujay
Certified Tutor

View Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

All ISEE Middle Level Math Resources

6 Diagnostic Tests 303 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Seattle, Calculus Tutors in Denver, Algebra Tutors in San Francisco-Bay Area, Reading Tutors in Washington DC, SAT Tutors in Phoenix, GMAT Tutors in Dallas Fort Worth, SAT Tutors in New York City, Math Tutors in Washington DC, ACT Tutors in Phoenix, ACT Tutors in Boston

Popular Courses & Classes

ACT Courses & Classes in Boston, ISEE Courses & Classes in Washington DC, ISEE Courses & Classes in Philadelphia, GRE Courses & Classes in New York City, SAT Courses & Classes in New York City, SSAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Chicago, MCAT Courses & Classes in Atlanta, ACT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Chicago

Popular Test Prep

SSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Dallas Fort Worth, GRE Test Prep in Miami, SAT Test Prep in Boston, SSAT Test Prep in Boston, LSAT Test Prep in Dallas Fort Worth, SAT Test Prep in Miami, SSAT Test Prep in Miami, ACT Test Prep in San Francisco-Bay Area, SAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Middle Level Math : Geometry

Study concepts, example questions & explanations for ISEE Middle Level Math

All ISEE Middle Level Math Resources

Example Questions

Example Question #3 : How To Find The Perimeter Of A Parallelogram

Example Question #1303 : Concepts

Example Question #1 : Parallelograms

Example Question #1 : How To Find The Area Of A Parallelogram

Example Question #1 : How To Find The Area Of A Parallelogram

Example Question #2 : How To Find The Area Of A Parallelogram

Example Question #3 : How To Find The Area Of A Parallelogram

Example Question #2 : Parallelograms

Example Question #1 : How To Find A Square On A Coordinate Plane

Example Question #1 : How To Find The Points On A Coordinate Plane

All ISEE Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: