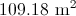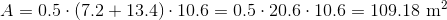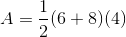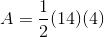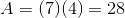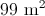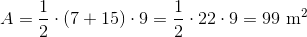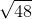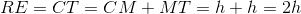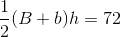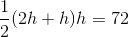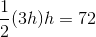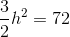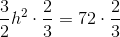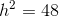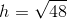All ISEE Middle Level Math Resources
Example Questions
Example Question #251 : Geometry
Use the following rectangle to answer the question:
Find the perimeter.
To find the perimeter of a rectangle, we will use the following formula:
Where a, b, c, and d are the lengths of the sides of the rectangle.
Now, given the rectangle,
we can see the length is 9cm. Because it is a rectangle, the opposite side is also 9cm.
We can see the width is 7cm. Because it is a rectangle, the opposite side is also 7cm.
Knowing this, we can substitute into the formula. We get
Example Question #252 : Geometry
Find the perimeter of a rectangle with a width of 6in and a length that is three times the width.
To find the perimeter of a rectangle, we will use the following formula:
Where a, b, c, and d are the lengths of the sides of the rectangle.
Now, we know the width of the rectangle is 6in. Because it is a rectangle, the opposite side is also 6in.
We know the length is three times the width. Therefore, the length is 18in. Because it is a rectangle, the opposite side is also 18in.
So, we can substitute. We get
Example Question #253 : Geometry
Find the perimeter of a rectangle with a width of 4cm and a length that is three times the width.
To find the perimeter of a rectangle, we will use the following formula:
Where a, b, c, and d are the lengths of the sides of the rectangle.
Now, we know the width of the rectangle is 4cm. Because it is a rectangle, the opposite side is also 4cm.
We know the length is three times the width. Therefore, the length is 12cm. Because it is a rectangle, the opposite side is also 12cm.
So, we can substitute.
Example Question #254 : Geometry
Find the perimeter of a rectangle with a width of 6in and a length that is two times the width.
To find the perimeter of a rectangle, we will use the following formula:
Where a, b, c, and d are the lengths of the sides of the rectangle.
Now, we know the width of the rectangle is 6in. Because it is a rectangle, the opposite side is also 6in.
We know the length is two times the width. Therefore, the length is 12in. Because it is a rectangle, the opposite side is also 12in.
So, we get
Example Question #255 : Geometry
Find the perimeter of a rectangle with a length of 16cm and a width that is a quarter of the length.
To find the perimeter of a rectangle, we will use the following formula:
Where a, b, c, and d are the lengths of the sides of the rectangle.
Now, we know the length of the rectangle is 16cm. Because it is a rectangle, the opposite side is also 16cm. We also know the width of the rectangle is a quarter of the length. To find the width, we will divide 16 by 4. Therefore, the width is 4cm. Because it is a rectangle, the opposite side is also 4cm.
Knowing this, we can substitute into the formula. We get
Example Question #256 : Geometry
Find the perimeter of a rectangle with an area of 

This problem requires finding the height of the rectangle first.
Write the formula for the area of the rectangle, and substitute the known values.
Divide by two on both sides to obtain the height.
The perimeter of a rectangle includes 2 bases and 2 heights.
The formula for the perimeter is:
Substitute the values to find the perimeter.
The perimeter is:
Example Question #1 : How To Find The Area Of A Trapezoid
What is the area of the above trapezoid?
To find the area of a trapezoid, multiply one half (or 0.5, since we are working with decimals) by the sum of the lengths of its bases (the parallel sides) by its height (the perpendicular distance between the bases). This quantity is
Example Question #1 : How To Find The Area Of A Trapezoid
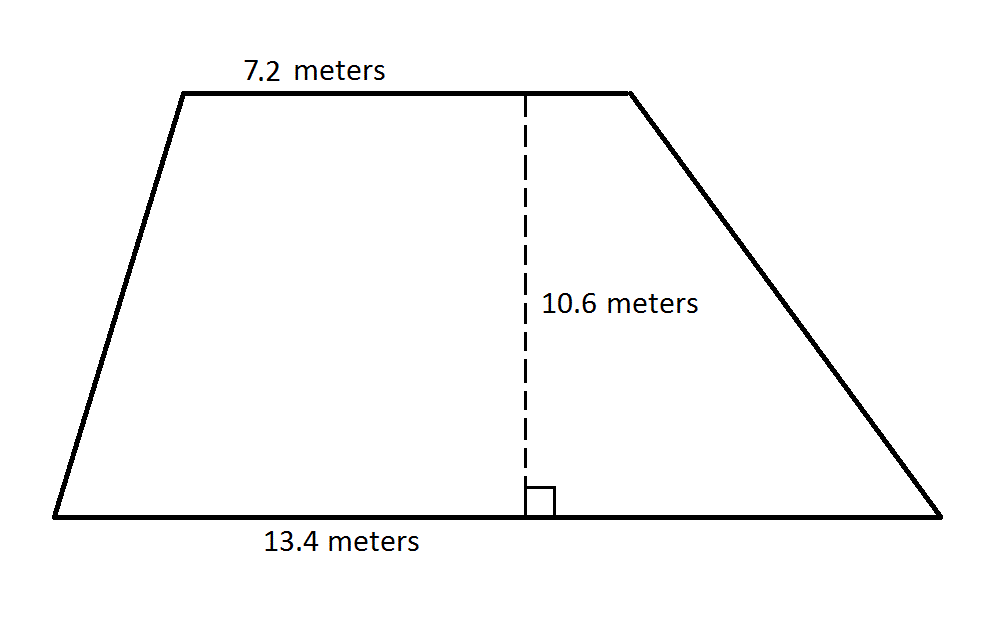
Find the area of the trapezoid:
The area of a trapezoid can be determined using the equation 
Example Question #1221 : Concepts
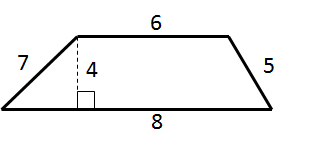
What is the area of the trapezoid?
To find the area of a trapezoid, multiply the sum of the bases (the parallel sides) by the height (the perpendicular distance between the bases), and then divide by 2.
Example Question #1231 : Concepts
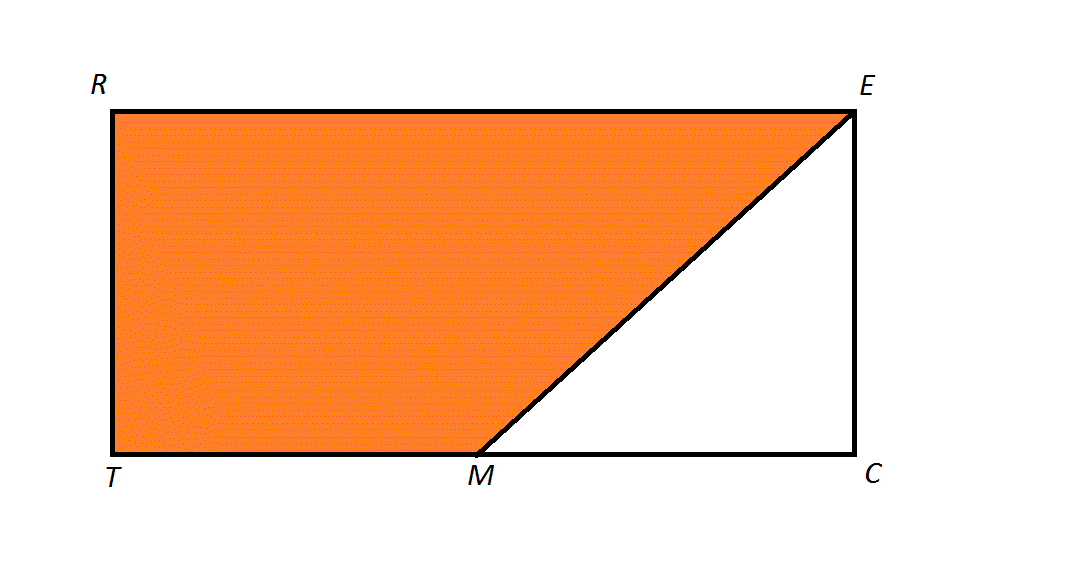
The above diagram depicts a rectangle 





The length of a leg of 

Since the triangle is isosceles, then 



Therefore, the orange region is a trapezoid with bases 


This is the length of one leg of the triangle.
Certified Tutor
All ISEE Middle Level Math Resources