Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Lower Level Quantitative : How to use a Venn Diagram

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

Create An Account

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #6 : How To Find The Common Part With A Venn Diagram

If Jill likes blue, yellow, tan and green, and Doug likes red, tan, black and green, which Venn diagram is correct?

Possible Answers:

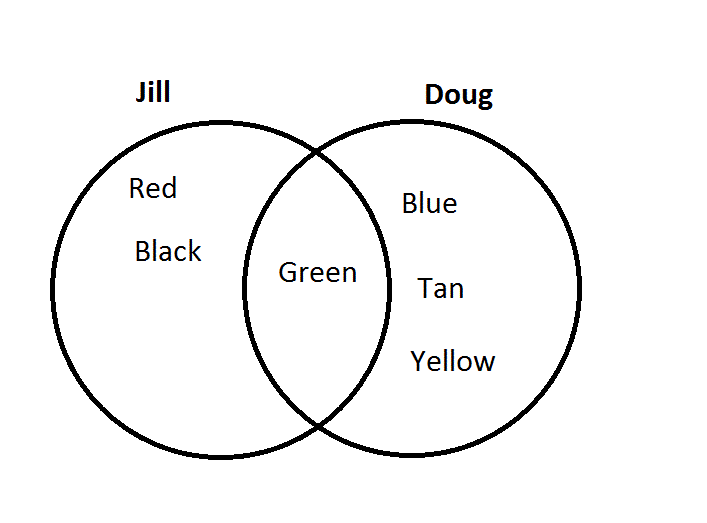
Venn3

Venn4

Venn2

Venn1

Venn5

Correct answer:

Venn1

Explanation:

The middle portion of the diagram is the area that both circles share, so the color name that belongs in both circles should go in the middle area. Doug and Jill both like green and tan, so those colors should go in the middle. Only Jill likes blue and yellow, so these go on Jill's side. Only Doug likes red and black, so these go on Doug's side.

Report an Error

Example Question #2 : How To Use A Venn Diagram

The following Venn diagram depicts the number of students who like soccer, football, or both. How many students like soccer but not football?

Possible Answers:

Correct answer:

Explanation:

A Venn diagram is used to demonstrate the number of people (or things) in particular categories. The regions of the circle that are overlapping indicate the number of individuals that belong to multiple groups. Therefore, based on this diagram, 12 students like soccer only, 16 like football only, and 8 like both.

Report an Error

Example Question #3 : Venn Diagrams

Custom_vt_venn_d._lower_level_isee.gif6

The Venn diagram above represents the results from a recent survey given to middle school students. Category $\small A$ represents the amount of students that only like pizza. Category $\small B$ represents the amount of students that only chicken nuggets.

What fraction of the students only like chicken nuggets?

Possible Answers:

$\small \frac{5}{100}$

$\small \frac{7}{20}$

$\small \frac{30}{100}$

$\small \frac{100}{35}$

Correct answer:

$\small \frac{7}{20}$

Explanation:

Since exactly $\small 35$ of a total $\small 100$ percent of the students only like chicken nuggets, the solution is:
$\small \frac{35}{100}=\frac{7}{20}$

Report an Error

Example Question #43 : Data Analysis

Custom_vt_venn_d._lower_level_isee.gif6

Possible Answers:

$\small \frac{13}{100}$

$\small \frac{35}{100}$

$\small \frac{6}{50}$

$\small \frac{3}{5}$

Correct answer:

$\small \frac{13}{100}$

Explanation:

Since category $\small A$ represents the total number of students that only like pizza, the correct answer is that $\small 13$ percent is equivalent to $\small \frac{13}{100}$ .

Report an Error

Example Question #44 : Data Analysis

Custom_vt_venn_d._lower_level_isee.gif_2

Aracely posted a survey question using one of her social network accounts. She grouped the results into three categories. The response results are represented by the Venn diagram shown above.

Group $\small A$ represents the respondents that answered "yes" to the survey question. Group $\small B$ represents the respondents that answered "no" to the survey question. And, the overlapping part of the diagram represents the respondents that answered "maybe" to the survey question.

What percentage of the respondents answered "no" to Aracely's survey question?

Possible Answers:

$20\%$

$35\%$

$55\%$

$45\%$

Correct answer:

$35\%$

Explanation:

The Venn diagram has three separate categories. Category $\small A$ represents the respondents that answered "yes" to the survey question, category $\small B$ represents the respondents that answered "no" and the overlapping portion of the diagram represents the respondents that answered "maybe" to the survey question.

Category $\small B=35\%$ .

Thus, $\small 35\%$ of the respondents answered "no" to the survey question.

Report an Error

Example Question #1 : How To Use A Venn Diagram

Custom_vt_venn_d._lower_level_isee.gif_2

Aracely posted a survey question using one of her social network accounts. She grouped the results into three categories. The response results are represented by the Venn diagram shown above.

Group $\small A$ represents the respondents that answered "yes" to the survey question. Group $\small B$ represents the respondents that answered "no" to the survey question. And, the overlapping part of the diagram represents the respondents that answered "maybe" to the survey question.

What fraction represents the amount of respondents that answered "yes" to the survey question?

Possible Answers:

$\small \frac{1}{5}$

$\small \frac{2}{5}$

$\small \frac{4}{10}$

$\small \frac{1}{4}$

Correct answer:

$\small \frac{1}{5}$

Explanation:

The Venn diagram shows that exactly $\small 20$ percent of the survey respondents answered "yes" to the survey question.

Thus, to find the fraction equivalent we need to rewrite

$20\% \rightarrow \frac{20}{100}$

From here we simplify the fraction.

$\frac{20}{100}=\frac{2}{10}=\frac{1}{5}$

Report an Error

Example Question #1 : How To Use A Venn Diagram

Custom_vt_venn_d._lower_level_isee.gif_lp

The Venn diagram shown above has three categories that represent information about the Wildcats varsity baseball team.

Category $\small L$ represents the number of players on the team that are left-handed.
Category $\small P$ represents the numebr of players on the team that are pitchers.
And, the overlapping portion of the Venn diagram represents the number of players that are left-handed pitchers.

Given that $\small L=6, P=9$ and that there are $\small 3$ players in the overlapping region of the diagram.

How many players are right-handed pitchers?

Possible Answers:

Correct answer:

Explanation:

Since the question provides the information that there are $\small 3$ left-handed pitchers and $\small 9$ total pitchers, one can infer that the number of right-handed pitchers is equal to the difference between the total number of pitchers and the number of left-handed pitchers.

Thus, the solution is:

9-3=6

Report an Error

Example Question #3 : How To Use A Venn Diagram

Custom_vt_venn_d._lower_level_isee.gif_lp

Possible Answers:

$\small \frac{4}{5}$

$\small \frac{1}{5}$

$\small \frac{3}{6}$

$\small \frac{1}{6}$

Correct answer:

$\small \frac{1}{5}$

Explanation:

Since, there are $\small 6$ left-handed players total and $\small 3$ left-handed pitchers there must be $\small 3$ players that are left-handed but do not pitch, because $\small 6-3=3$ .

To find what fraction this represents we need to do:

$\frac{\text{left handed}}{\text{total players}}=\frac{3}{15}=\frac{1}{5}$

Report an Error

Example Question #52 : Data Analysis

Custom_vt_venn_d._lower_level_isee.gif3

In the above Venn diagram category $\small A$ represents the number of Kevin's friends that play the flute, while category $\small B$ represents the number of Kevin's friends that play the bass.

If $\small \frac{2}{8}$ of Kevin's friends only play the flute and $\small \frac{2}{8}$ of his friends only play the bass, then what fraction of Kevin's friends play both instruments?

Possible Answers:

$\small \frac{2}{3}$

$\small \frac{6}{8}$

$\small \frac{2}{8}$

$\small \frac{1}{2}$

Correct answer:

$\small \frac{1}{2}$

Explanation:

To find the fraction of Kevin's friends that play both the bass and the flute, consider that the fraction $\small \frac{8}{8}$ represents all of Kevin's friends in this senario.

Thus, the solution can be found by adding those that only play flute with those that only play bass and subtracting that final answer from the fraqction that represents all of Kevin's friends:

$\small \small \frac{2}{8}+\frac{2}{8}=\frac{4}{8}$

$\frac{8}{8}-\frac{4}{8}=\frac{8-4}{8}=\frac{4}{8}=\frac{1}{2}$

Report an Error

Example Question #1661 : Isee Lower Level (Grades 5 6) Quantitative Reasoning

Custom_vt_venn_d._lower_level_isee.gif3

Possible Answers:

$15\%$

$20\%$

$25\%$

$40\%$

Correct answer:

$25\%$

Explanation:

$\small \frac{2}{8}$ of Kevin's friends only play the bass.

Thus, to find the fractional equivalent we need to multiply the fraction by 100.

The solution becomes:

$\frac{2}{8}\times100 = \frac{200}{8}=\frac{25}{1}= 25$

Report an Error

View Tutors

Danielle
Certified Tutor

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Julie
Certified Tutor

Université de Montréal, Professional (JD, MD, DMD, etc), Early Childhood.

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Philadelphia, MCAT Tutors in Seattle, Algebra Tutors in Seattle, Reading Tutors in Miami, Statistics Tutors in Miami, ACT Tutors in Boston, Physics Tutors in Boston, Biology Tutors in Philadelphia, GRE Tutors in Seattle, MCAT Tutors in Houston

Popular Courses & Classes

GMAT Courses & Classes in Houston, Spanish Courses & Classes in Seattle, GMAT Courses & Classes in Seattle, SSAT Courses & Classes in Phoenix, GRE Courses & Classes in Seattle, MCAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Washington DC, MCAT Courses & Classes in Denver, LSAT Courses & Classes in New York City, ACT Courses & Classes in Atlanta

Popular Test Prep

ISEE Test Prep in San Diego, MCAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Philadelphia, GMAT Test Prep in Denver, ACT Test Prep in Atlanta, GMAT Test Prep in Chicago, LSAT Test Prep in New York City, SSAT Test Prep in Boston, LSAT Test Prep in Boston, GMAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Lower Level Quantitative : How to use a Venn Diagram

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

All ISEE Lower Level Quantitative Resources

Example Questions

Example Question #6 : How To Find The Common Part With A Venn Diagram

Example Question #2 : How To Use A Venn Diagram

Example Question #3 : Venn Diagrams

Example Question #43 : Data Analysis

Example Question #44 : Data Analysis

Example Question #1 : How To Use A Venn Diagram

Example Question #1 : How To Use A Venn Diagram

Example Question #3 : How To Use A Venn Diagram

Example Question #52 : Data Analysis

Example Question #1661 : Isee Lower Level (Grades 5 6) Quantitative Reasoning

All ISEE Lower Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: