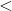All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #1 : Compare Two Fractions With Different Numerators And Different Denominators: Ccss.Math.Content.4.Nf.A.2
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #2 : Compare Two Fractions With Different Numerators And Different Denominators: Ccss.Math.Content.4.Nf.A.2
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #391 : Number Concepts And Operations
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #1 : Compare Two Fractions With Different Numerators And Different Denominators: Ccss.Math.Content.4.Nf.A.2
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #392 : Number Concepts And Operations
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #1 : How To Compare Fractions
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #332 : Rational Numbers
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #334 : Rational Numbers
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #3 : Compare Two Fractions With Different Numerators And Different Denominators: Ccss.Math.Content.4.Nf.A.2
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #1691 : Numbers And Operations
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Certified Tutor
All ISEE Lower Level Quantitative Resources