All Intermediate Geometry Resources
Example Questions
Example Question #81 : Parallelograms
In the figure, the area of the parallelogram is 


Recall how to find the area of a parallelogram:
Now, substitute in the area, base, and height values that are given by the question.
Expand this equation.
Now factor this equation.
Solve for 
Since lengths of bases and heights can only be positive, 
Notice that the length of the base is given by the expression 

Example Question #82 : Parallelograms
In the figure, the area of the parallelogram is 


Recall how to find the area of a parallelogram:
Now, substitute in the area, base, and height values that are given by the question.
Expand this equation.
Now factor this equation.
Solve for 
Since lengths of bases and heights can only be positive, 
Notice that the length of the base is given by the expression 

Example Question #83 : Parallelograms
In the figure, the area of the parallelogram is 


Recall how to find the area of a parallelogram:
Now, substitute in the area, base, and height values that are given by the question.
Expand this equation.
Now factor this equation.
Solve for 
Since lengths of bases and heights can only be positive, 
Notice that the length of the base is given by the expression 

Example Question #41 : How To Find The Area Of A Parallelogram
In the figure, the area of the parallelogram is 


Recall how to find the area of a parallelogram:
Now, substitute in the area, base, and height values that are given by the question.
Expand this equation.
Now factor this equation.
Solve for 
Since lengths of bases and heights can only be positive, 
Notice that the length of the base is given by the expression 

Example Question #42 : How To Find The Area Of A Parallelogram
In the figure, the area of the parallelogram is 


Recall how to find the area of a parallelogram:
Now, substitute in the area, base, and height values that are given by the question.
Expand this equation.
Now factor this equation.
Solve for 
Since lengths of bases and heights can only be positive, 
Notice that the length of the base is given by the expression 

Example Question #81 : Parallelograms
Find the area of the parallelogram.


Recall how to find the area of a parallelogram:
From the given parallelogram, we will need to use the Pythagorean Theorem to find the length of the height of the parallelogram.
Plug in the given values to find the length of the height.
Now, use the height to find the area of the parallelogram.
Remember to round to 
Example Question #82 : Parallelograms
Find the area of the parallelogram.


Recall how to find the area of a parallelogram:
From the given parallelogram, we will need to use the Pythagorean Theorem to find the length of the height of the parallelogram.
Plug in the given values to find the length of the height.
Now, use the height to find the area of the parallelogram.
Remember to round to 
Example Question #45 : How To Find The Area Of A Parallelogram
Find the area of the parallelogram.


Recall how to find the area of a parallelogram:
From the given parallelogram, we will need to use the Pythagorean Theorem to find the length of the height of the parallelogram.
Plug in the given values to find the length of the height.
Now, use the height to find the area of the parallelogram.
Remember to round to 
Example Question #46 : How To Find The Area Of A Parallelogram
Find the area of the parallelogram.
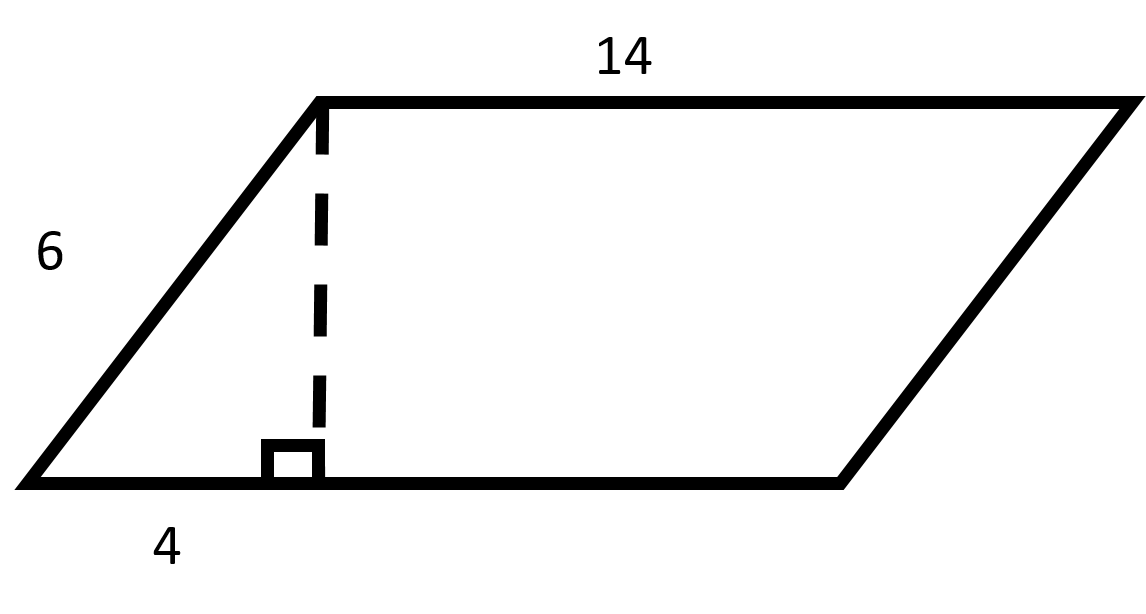

Recall how to find the area of a parallelogram:
From the given parallelogram, we will need to use the Pythagorean Theorem to find the length of the height of the parallelogram.
Plug in the given values to find the length of the height.
Now, use the height to find the area of the parallelogram.
Remember to round to 
Example Question #83 : Parallelograms
Find the area of the parallelogram.


Recall how to find the area of a parallelogram:
From the given parallelogram, we will need to use the Pythagorean Theorem to find the length of the height of the parallelogram.
Plug in the given values to find the length of the height.
Now, use the height to find the area of the parallelogram.
Remember to round to 
Certified Tutor
All Intermediate Geometry Resources























































































































