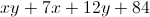All Intermediate Geometry Resources
Example Questions
Example Question #201 : Quadrilaterals
A paralellogram as two angles that are 65 degrees and 115 degrees respectively. What are the other two angles in the paralellogram?
This question is very simple to answer if you remember that ALL paralellograms have two pairs of equal and opposite angles, and that the four angles in any quadrilateral MUST add up to 360 degrees.
Because the angles given are different, we know that they are supplementary and the other two missing angles MUST be the same.
Example Question #202 : Quadrilaterals
Given: Regular Pentagon 




True or false: Quadrilateral 
True
False
False
Below is regular Pentagon 



The measure of each angle of a regular pentagon can be calculated by setting 
and evaluating:
Specifically,
By symmetry, each radius bisects one of these angles. Specifically,
By the Same-Side Interior Angles Theorem, consecutive angles of a parallelogram are supplementary - that is, their measures total 

violating these conditions. Therefore, Quadrilateral 
Example Question #203 : Quadrilaterals
Given: Quadrilateral 


True or false: It follows that Quadrilateral 
True
False
False






Example Question #204 : Quadrilaterals
Given: Parallelogram 


True or false: It follows that Parallelogram 
False
True
True
By the Same-Side Interior Angles Theorem, consecutive angles of a parallelogram can be proved to be supplementary - that is, their angle measures total 




Example Question #31 : Parallelograms
Given: Rectangle 



True or false: 
True
False
False
The diagonals of a parallelogram are perpendicular - and, consequently, 

Example Question #371 : Intermediate Geometry
Given: Parallelogram 

True or false: Parallelogram 
False
True
True
A rectangle is a parallelogram with four right angles.
Consecutive angles of a parallelogram are supplementary. If one angle of a parallelogram is given to be right, then its neighboring angles, being supplementary to a right angle, are right as well; also, opposite angles of a parallelogram are congruent, so the opposite angle is also right. All four angles must be right, making the parallelogram a rectangle by definition.
Example Question #203 : Quadrilaterals
Find the perimeter of the following box in inches:

The answer is 
You can find the perimeter by adding all of its respective sides as such:

Adding like terms will result in
If you chose 
If you chose 
Just remember, the width is 12 added to 

Example Question #1 : How To Find The Length Of The Side Of A Parallelogram
A parallelogram has an area of 

Cannot be determined
If the area of a parallelogram is given as 




This very quickly becomes a problem of substituting in values and finding the value of an unknown variable, in this case, 
Example Question #1 : How To Find The Length Of The Side Of A Parallelogram
A parallelogram has a base of 






In order to find the height of this parallelogram apply the formula:
Example Question #210 : Quadrilaterals
A parallelogram has a height of 






To find the missing side of this parallelgram apply the formula:
Thus, the solution is:
All Intermediate Geometry Resources