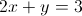We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Perpendicular Lines

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 Next →

Example Question #1 : How To Find The Equation Of A Perpendicular Line

What line is perpendicular to $y=\frac{-1}{2}x-3$ through (1,5) ?

Possible Answers:

2x-y = -3

x+3y=1

2x+y=3

3x-y=4

x-y=5

Correct answer:

2x-y = -3

Explanation:

$y=\frac{-1}{2}x-3$ is given in the slope-intercept form. So the slope is $\frac{-1}{2}$ and the y-intercept is .

If the lines are perpendicular, then $m_{1}\cdot m_{2}=-1$ so the new slope must be

Next we substitute the new slope and the given point into the slope-intercept form of the equation to calculate the intercept. So the equation to solve becomes 5=2(1) +b so b=3

So the equation of the perpendicular line becomes y=2x+3 or in standard form 2x-y=-3

Report an Error

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Which line below is perpendicular to 5x+6y=18 ?

Possible Answers:

$y=-\frac{6}{5}x+8$

$y=-\frac{5}{6}x+\frac{6}{5}$

$y=\frac{5}{6}x+2$

$y=\frac{5}{6}x+\frac{6}{5}$

$y = \frac{6}{5}x + 3$

Correct answer:

$y = \frac{6}{5}x + 3$

Explanation:

The definition of a perpendicular line is one that has a negative, reciprocal slope to another.

For this particular problem, we must first manipulate our initial equation into a more easily recognizable and useful form: slope-intercept form or y=mx+b .

5x+6y=18

6y=-5x+18

$y=-\frac{5}{6}x+6$

According to our y=mx+b formula, our slope for the original line is $-\frac{5}{6}$ . We are looking for an answer that has a perpendicular slope, or an opposite reciprocal. The opposite reciprocal of $-\frac{5}{6}$ is $\frac{6}{5}$ . Flip the original and multiply it by .

Our answer will have a slope of $\frac{6}{5}$ . Search the answer choices for $\frac{6}{5}$ in the position of the y=mx+b equation.

$\dpi{100} y = \frac{6}{5}x + 3$ is our answer.

(As an aside, the negative reciprocal of 4 is $-\frac{1}{4}$ . Place the whole number over one and then flip/negate. This does not apply to the above problem, but should be understood to tackle certain permutations of this problem type where the original slope is an integer.)

Report an Error

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Find the equation of the line perpendicular to $y=\frac{-1}{3}x+2$ .

Possible Answers:

y=3x-2

y=-3x-2

y=3x+2

$y=\frac{1}{3}x+2$

y=-3x+2

Correct answer:

y=3x+2

Explanation:

The definition of a perpendicular line is a line with a negative reciprocal slope and identical intercept.

Therefore we need a line with slope 3 and intercept 2.

This means the only fitting line is y=3x+2 .

Report an Error

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Which one of these equations is perpendicular to:

y=x+2

Possible Answers:

y=2

y=-x+1

y=-2x+5

y=-x^2

y=x

Correct answer:

y=-x+1

Explanation:

To find the perpendicular line to

y=x+2

we need to find the negative reciprocal of the slope of the above equation.

So the slope of the above equation is since changes by when is incremented.

The negative reciprocal is:

$reciprocal=\frac{-1}{slope}$

$reciprocal=\frac{1}{-1}$

reciprocal=-1

So we are looking for an equation with a .

Only y=-x+1 satisfies this condition.

Report an Error

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Suppose a line is represented by a function f(x) = 2x+4 . Find the equation of a perpendicular line that intersects the point (1,2) .

Possible Answers:

$f(x)= \frac{1}{2}x-1\frac{1}{2}$

$f(x)= -\frac{1}{2}x+1\frac{1}{2}$

$f(x)= -\frac{1}{2}x$

f(x)=2x

$f(x)= -\frac{1}{2}x+2\frac{1}{2}$

Correct answer:

$f(x)= -\frac{1}{2}x+2\frac{1}{2}$

Explanation:

Determine the slope of the function f(x) = 2x+4 . The slope is: m1=2

The slope of a perpendicular line is the negative reciprocal of the original slope. Determine the value of the slope perpendicular to the original function.

$m2 = - \frac{1}{m1} = -\frac{1}{2}$

Plug in the given point and the slope to the slope-intercept form to find the y-intercept.

y=mx+b

$2=\left(-\frac{1}{2}\right)(1)+b$

$b=2\frac{1}{2}$

Substitute the slope of the perpendicular line and the new y-intercept back in the slope-intercept equation, y=mx+b .

The correct answer is: $f(x)= -\frac{1}{2}x+2\frac{1}{2}$

Report an Error

Example Question #5 : How To Find The Equation Of A Perpendicular Line

Suppose a perpendicular line passes through y=2x-1 and point (-1,5) . Find the equation of the perpendicular line.

Possible Answers:

$y=-\frac{1}{2}x+4\frac{1}{2}$

y=-2x+3

$y=-\frac{1}{2}x-4\frac{1}{2}$

y=-2x-7

$y=\frac{1}{2}x+5\frac{1}{2}$

Correct answer:

$y=-\frac{1}{2}x+4\frac{1}{2}$

Explanation:

Find the slope from the given equation y=2x-1 . The slope is: m1=2 .

The slope of the perpendicular line is the negative reciprocal of the original slope.

$m2=-\frac{1}{m1}=-\frac{1}{2}$

Plug in the perpendicular slope and the given point to the slope-intercept equation.

y=mx+b

$5=\left(-\frac{1}{2}\right)(-1)+b$

$5=\frac{1}{2}+b$

$b=4\frac{1}{2}$

Plug in the perpendicular slope and the y-intercept into the slope-intercept equation to get the equation of the perpendicular line.

$y=-\frac{1}{2}x+4\frac{1}{2}$

Report an Error

Example Question #6 : How To Find The Equation Of A Perpendicular Line

Find a line perpendicular y=6x-5 , but passing through the point (7,2) .

Possible Answers:

$y=-\frac{1}{6}x-\frac{19}{6}$

$y=6x+\frac{19}{6}$

$y=-\frac{1}{6}x+\frac{19}{6}$

$y=\frac{1}{6}x-\frac{19}{6}$

$y=6x-\frac{19}{6}$

Correct answer:

$y=-\frac{1}{6}x+\frac{19}{6}$

Explanation:

Since we need a line perpendicular to y=6x-5 we know our slope must be $m=-\frac{1}{6}$ . This is because perpendicular lines have slopes that are negative reciprocals of each other. In order for our new line to pass through the point (7,2) we must use the point slope formula. Be sure to use the perpendicular slope.

$y-y_{1}=m(x-x_{1})$

$y-2=\frac{-1}{6}(x-7)$

$y=\frac{-1}{6}x+\frac{7}{6}+2$

$y=\frac{-1}{6}x+\frac{7}{6}+\frac{12}{6}$

$\mathbf{y=-\frac{1}{6}x+\frac{19}{6}}$

Report an Error

Example Question #7 : How To Find The Equation Of A Perpendicular Line

A line is perpendicular to the line of the equation

5x+ 7y = 32

and passes through the point (-2, 8) .

Give the equation of the line.

Possible Answers:

$\textup{None of the other choices gives the correct response}$

5x- 7y = -66

7x + 5y= 26

7x- 5y= -54

5x+ 7y = 46

Correct answer:

7x- 5y= -54

Explanation:

A line perpendicular to another line will have as its slope the opposite of the reciprocal of the slope of the latter. Therefore, it is necessary to find the slope of the line of the equation

5x+ 7y = 32

Rewrite the equation in slope-intercept form y = mx+ b . , the coefficient of , will be the slope of the line.

Add -5x to both sides:

5x+ 7y + (-5x ) = 32 + (-5x )

7y = -5x+32

Multiply both sides by $\frac{1}{7}$ , distributing on the right:

$\frac{1}{7} \cdot 7y = \frac{1}{7} \cdot( -5x+32)$

$y = -\frac{5}{7}x+\frac{32}{7}$

The slope of this line is $-\frac{5}{7}$ . The slope of the first line will be the opposite of the reciprocal of this, or $\frac{7}{5}$ . The slope-intercept form of the equation of this line will be

$y = \frac{7}{5}x+b$ .

To find , set x = -2 and y = 8 and solve:

$8 = \frac{7}{5} (-2)+b$

$8 = - \frac{14}{5} +b$

$\frac{40}{5} = - \frac{14}{5} +b$

Add $\frac{14}{5}$ to both sides:

$\frac{40}{5} + \frac{14}{5} = - \frac{14}{5} +b + \frac{14}{5}$

$\frac{54}{5} = b$

The equation, in slope-intercept form, is $y = \frac{7}{5}x+ \frac{54}{5}$ .

To rewrite in standard form with integer coefficients:

Multiply both sides by 5:

$5 y =5 \left (\frac{7}{5}x+ \frac{54}{5} \right )$

$5 y =5 \left (\frac{7}{5}x \right ) + 5 \left ( \frac{54}{5} \right )$

5 y =7x+54

Add -5y-54 to both sides:

5 y + (-5y-54) =7x+54 + (-5y-54)

-54 =7x -5y

7x -5y = -54

Report an Error

Example Question #1 : How To Find The Slope Of A Perpendicular Line

Any line that is perpendicular to 18-9y=13x must have a slope of what?

Possible Answers:

-13/9

-9/13

1/2

13/9

9/13

Correct answer:

9/13

Explanation:

Two lines are perpendicular if and only if their slopes are negative reciprocals of each other. To find the slope, we must put the equation into slope-intercept form, y=mx+b , where equals the slope of the line. First, we must subtract from both sides of the equation, giving us -9y=13x-18 . Next, we must divide both sides by , giving us y=-13x/9+2 . We can now see that the slope of this line is -13/9 . Therefore, any line that is perpendicular to this one must have a slope of 9/13 .

Report an Error

Example Question #1 : How To Find The Slope Of A Perpendicular Line

What is the slope of any line perpendicular to $y=-\frac{1}{2}x+5$ ?

Possible Answers:

$-\frac{1}{2}$

$\frac{1}{2}$

Correct answer:

Explanation:

The slope of a perpendicular line is the negative reciprocal of the original slope.

The original slope is $-\frac{1}{2}$ .

The negative reciprocal of the original slope is:

$-\frac{1}{-(\frac{1}{2})} = 2$

Report an Error

← Previous 1 2 3 Next →

View Tutors

Musab Ahamed
Certified Tutor

View Tutors

Abhisek
Certified Tutor

University of Florida, Bachelor of Engineering, Computer Science.

View Tutors

Najwan
Certified Tutor

CUNY New York City College of Technology, Bachelor of Science, Mechanical Engineering Technology.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in New York City, ACT Tutors in San Diego, Spanish Tutors in Phoenix, Computer Science Tutors in Philadelphia, Chemistry Tutors in Philadelphia, Chemistry Tutors in New York City, Algebra Tutors in San Diego, LSAT Tutors in Chicago, MCAT Tutors in Houston, Chemistry Tutors in San Diego

Popular Courses & Classes

ISEE Courses & Classes in Los Angeles, Spanish Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Philadelphia, GRE Courses & Classes in Phoenix, SSAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Chicago, GMAT Courses & Classes in New York City, Spanish Courses & Classes in Philadelphia, SAT Courses & Classes in Phoenix

Popular Test Prep

GMAT Test Prep in Chicago, GRE Test Prep in New York City, GRE Test Prep in Seattle, MCAT Test Prep in Washington DC, ACT Test Prep in Philadelphia, GRE Test Prep in Denver, SSAT Test Prep in Chicago, ACT Test Prep in Chicago, GRE Test Prep in Atlanta, SSAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Perpendicular Lines

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Example Question #5 : How To Find The Equation Of A Perpendicular Line

Example Question #6 : How To Find The Equation Of A Perpendicular Line

Example Question #7 : How To Find The Equation Of A Perpendicular Line

Example Question #1 : How To Find The Slope Of A Perpendicular Line

Example Question #1 : How To Find The Slope Of A Perpendicular Line

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: