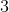We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #57 : Cylinders

A cylinder is cut in half and placed on top of a rectangular prism as shown by the figure below.

Possible Answers:

2241.20

2444.09

2590.15

2385.40

Correct answer:

2385.40

Explanation:

In order to find the volume of the figure, we will first need to find the volumes of the rectangular prism and the half cylinder.

From the figure, you should notice that the length of the prism is also the diameter of the half cylinder. Thus, half the length of the prism will also be the radius of the half cylinder. Also, notice that the width of the prism will be the height of the cylinder.

For the given cylinder then, find the radius.

$\text{radius}=\frac{\text{length}}{2}=\frac{10}{2}=5$

Then, recall how to find the volume of a cylinder:

$\text{Volume of Cylinder}=\pi r^2 h$ , where is the radius and is the height.

Divide the volume by to find the volume of the half cylinder.

$\text{Volume of Half Cylinder}=\frac{\pi r^2 h}{2}$

$\text{Volume of Half Cylinder}=\frac{\pi (5)^2(20)}{2}=250\pi$

Next, recall how to find the volume of a rectangular prism.

$\text{Volume of Rectangular Prism}=\text{length}\times\text{width}\times\text{height}$

Plug in the given values to find the volume of the rectangular prism.

$\text{Volume of Rectangular Prism}=(10)(20)(8)=1600$

To find the volume of the figure, add the volume of the half cylinder and the volume of the rectangular prism together.

$\text{Volume of Figure}=\text{Volume of Half Cylinder}+\text{Volume of Rectangular Prism}$

$\text{Volume of Figure}=250\pi+1600=2385.40$

Remember to round to places after the decimal.

Report an Error

Example Question #58 : Cylinders

A cylinder is cut in half and placed on top of a rectangular prism as shown by the figure below.

Possible Answers:

4449.12

4443.22

4333.71

4902.56

Correct answer:

4443.22

Explanation:

In order to find the volume of the figure, we will first need to find the volumes of the rectangular prism and the half cylinder.

For the given cylinder then, find the radius.

$\text{radius}=\frac{\text{length}}{2}=\frac{13}{2}$

Then, recall how to find the volume of a cylinder:

$\text{Volume of Cylinder}=\pi r^2 h$ , where is the radius and is the height.

Divide the volume by to find the volume of the half cylinder.

$\text{Volume of Half Cylinder}=\frac{\pi r^2 h}{2}$

$\text{Volume of Half Cylinder}=\frac{\pi (\frac{13}{2})^2(17)}{2}=\frac{2873}{8}\pi$

Next, recall how to find the volume of a rectangular prism.

$\text{Volume of Rectangular Prism}=\text{length}\times\text{width}\times\text{height}$

Plug in the given values to find the volume of the rectangular prism.

$\text{Volume of Rectangular Prism}=(13)(17)(15)=3315$

To find the volume of the figure, add the volume of the half cylinder and the volume of the rectangular prism together.

$\text{Volume of Figure}=\text{Volume of Half Cylinder}+\text{Volume of Rectangular Prism}$

$\text{Volume of Figure}=\frac{2873}{8}\pi+3315=4443.22$

Remember to round to places after the decimal.

Report an Error

Example Question #59 : Cylinders

A cylinder is cut in half and placed on top of a rectangular prism as shown by the figure below.

Find the volume of the figure.

Possible Answers:

32.56

34.09

31.11

33.93

Correct answer:

33.93

Explanation:

In order to find the volume of the figure, we will first need to find the volumes of the rectangular prism and the half cylinder.

For the given cylinder then, find the radius.

$\text{radius}=\frac{\text{length}}{2}=\frac{1}{2}$

Then, recall how to find the volume of a cylinder:

$\text{Volume of Cylinder}=\pi r^2 h$ , where is the radius and is the height.

Divide the volume by to find the volume of the half cylinder.

$\text{Volume of Half Cylinder}=\frac{\pi r^2 h}{2}$

$\text{Volume of Half Cylinder}=\frac{\pi (\frac{1}{2})^2(10)}{2}=\frac{5}{4}\pi$

Next, recall how to find the volume of a rectangular prism.

$\text{Volume of Rectangular Prism}=\text{length}\times\text{width}\times\text{height}$

Plug in the given values to find the volume of the rectangular prism.

$\text{Volume of Rectangular Prism}=(1)(10)(3)=30$

To find the volume of the figure, add the volume of the half cylinder and the volume of the rectangular prism together.

$\text{Volume of Figure}=\text{Volume of Half Cylinder}+\text{Volume of Rectangular Prism}$

$\text{Volume of Figure}=\frac{5}{4}\pi+30=33.93$

Remember to round to places after the decimal.

Report an Error

Example Question #60 : Cylinders

Inscribed

The above diagram shows a sphere inscribed inside a cylinder.

The sphere has a volume of 100. Give the volume of the cylinder.

Possible Answers:

125

$116\frac{1}{6}$

$133\frac{1}{3}$

120

150

Correct answer:

150

Explanation:

Let be the radius of the sphere. Then the radius of the base of the cylinder is also , and the height of the cylinder is h = 2r .

The volume of the cylinder is

$V_{1} = \pi r^{2} h$ ,

which, after substituting, is

$V _{1} = \pi r^{2} (2r)$

$V_{1} =2 \cdot \pi r^{2}\cdot r$

$V_{1} =2 \pi r^{3}$

The volume of the sphere is

$V_{2} = \frac{4}{3} \pi r^{3}$

Therefore, the ratio of the former to the latter is

$\frac{V_{1} }{V_{2}}=\frac{ 2 \pi r^{3}}{\frac{4}{3}\pi r^{3}}$

$\frac{V_{1} }{V_{2}}=\frac{ 2 }{\frac{4}{3} } = 2 \cdot \frac{3}{4} = \frac{3}{2}$

and

$V_{1} = \frac{3}{2}V_{2}$

That is, the volume of the cylinder is $\frac{3}{2}$ times that of the sphere, so the volume of the cylinder is

$V_{1} = \frac{3}{2} \cdot 100 = 150$ .

Report an Error

Example Question #61 : Cylinders

During a snow storm, 1670 m^3 of snow was collected. If the snow were put in a circular lot that had a radius of 30m , how high would the snow on the lot be?

Possible Answers:

$\text{Between 0 and 1 meter}$

$\text{Between 2 and 3 meters}$

$\text{Between 1 and 2 meters}$

$\text{Between 3 and 4 meters}$

Correct answer:

$\text{Between 0 and 1 meter}$

Explanation:

Since we are putting the snow on a circular base, we are dealing with a cylinder. Notice that the radius of the cylinder and the volume of the cylinder are already given to you.

Recall how to find the volume of a cylinder:

$\text{Volume}=\pi(\text{radius})^2(\text{height})$

Rearrange the equation to solve for the height:

$\text{Height}=\frac{\text{Volume}}{\pi(\text{radius})^2}$

Plug in the given volume and radius:

$\text{Height}=\frac{1670}{\pi(30)^2}=0.59m$

The height is between and meter.

Report an Error

Example Question #1 : How To Find The Length Of An Edge Of A Prism

The volume of a prism is 210m^3 .

Given the length is and the height is 5 m , find the width of the prism.

Possible Answers:

12 m

8 m

70 m

6 m

93 m

Correct answer:

6 m

Explanation:

The volume of a prism is length times width times height.

We are given the length is 7m and the width is 5m.

So, we plug these into our formula:

$7\cdot5\cdot height=210$ .

We then solve for height:

$height=\frac{210}{7\cdot5}=\frac{210}{35}=6$ .

The height is therefore 6m.

Report an Error

Example Question #1 : How To Find The Length Of An Edge Of A Prism

Find the missing edge of the prism when its volume is $600 \:units^3$ .

Find_the_edge

Possible Answers:

$10\:units$

$2\sqrt{61}$

15.6

$5\:units$

Correct answer:

$5\:units$

Explanation:

The goal is to find the height of the rectangular prism with the given information of its width and length. The volume of a rectangular prism is $V = w \cdot l \cdot h$ , where is width and is height.

Because we're given the final volume and two of the three variables, we can substitute in the information we know and solve for the missing variable.

$600= 10 \cdot 12 \cdot h$

$600= 120 \cdot h$

$\frac{600}{120}=h$

h=5

Therefore, the height of the prism is $5\:units$ .

Report an Error

Example Question #1 : How To Find The Length Of An Edge Of A Prism

A rectangular prism has a volume of 216 cubic meters. Its length is twice its width, and its height is twice its length. What is the length of the prism?

Possible Answers:

3 m

8 m

2 m

6 m

12 m

Correct answer:

6 m

Explanation:

If we let $\small w$ be the width of our prism, then since the length is twice the width, our length would be $\small 2w$ . Since the height is twice the length, our height would be $\small 4w$ .

Since the volume of a rectangular prism is simply the product of width, length, and height, we get

$\small V=lwh=w(2w)(4w)=8w^3=216$

We then simply solve for the width.

$\small 8w^3=216$

$\small w^3=27$

$\small w=3$

Therefore, our width is 3. Since our length is twice the width, the length is 6.

Report an Error

Example Question #2 : How To Find The Length Of An Edge Of A Prism

A right, rectangular prism has a volume of 240 cubic inches. Its width is inches and its height is inches. What is its length?

Possible Answers:

210in

48in

8in

16in

None of the other answers.

Correct answer:

8in

Explanation:

The formula for the volume of a right, rectangular prism is V=lwh , so substitute the known values and solve for lenght.

$240 = l(5)(6) \rightarrow 240 = 30l \rightarrow8 = l$ . So the length is 8 inches.

Report an Error

Example Question #1 : How To Find The Length Of An Edge Of A Prism

The surface area of a right rectangular prism is 358 square cm. Its length is cm and its height is cm. Find the width of the prism.

Possible Answers:

34.8cm

14.5cm

13.8cm

None of the other answers.

7cm

Correct answer:

7cm

Explanation:

Use the formula for finding the surface area of a right, rectangular prism,

SA = 2lw + 2wh + 2lh

and substitute the known values, and then solve for w.

So,

$358 = 2(12)(w) + 2(w)(5) + 2(12)(5) \rightarrow 358 = 24w + 10w + 120$

$\rightarrow 238 = 34w \rightarrow w = 7$

So, the width is 7 cm.

Report an Error

View Tutors

Godswill
Certified Tutor

Rivers State University, Bachelor of Engineering, Mechanical Engineering. Texas Southern University, Master of Science, Compu...

View Tutors

Joseph
Certified Tutor

Rutgers University-New Brunswick, Bachelor in Arts, Chemistry. Rutgers Graduate School of Biomedical Sciences, Current Grad S...

View Tutors

Ariel
Certified Tutor

Central Bicol State University of Agriculture, Doctor of Education, Child Development.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in New York City, Reading Tutors in Dallas Fort Worth, Computer Science Tutors in Philadelphia, ISEE Tutors in Washington DC, French Tutors in New York City, GRE Tutors in Denver, Physics Tutors in Houston, Biology Tutors in Phoenix, Math Tutors in Chicago, Math Tutors in San Francisco-Bay Area

Popular Courses & Classes

SAT Courses & Classes in Chicago, SAT Courses & Classes in San Diego, GRE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in San Diego, Spanish Courses & Classes in Los Angeles, LSAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Denver, SAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in San Diego

Popular Test Prep

GRE Test Prep in Denver, GRE Test Prep in Houston, LSAT Test Prep in Chicago, SAT Test Prep in Phoenix, SAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Philadelphia, LSAT Test Prep in Los Angeles, GMAT Test Prep in Seattle, LSAT Test Prep in San Diego, GMAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #57 : Cylinders

Example Question #58 : Cylinders

Example Question #59 : Cylinders

Example Question #60 : Cylinders

Example Question #61 : Cylinders

Example Question #1 : How To Find The Length Of An Edge Of A Prism

Example Question #1 : How To Find The Length Of An Edge Of A Prism

Example Question #1 : How To Find The Length Of An Edge Of A Prism

Example Question #2 : How To Find The Length Of An Edge Of A Prism

Example Question #1 : How To Find The Length Of An Edge Of A Prism

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: