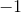We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : How to find the slope of a perpendicular line

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Perpendicular Lines

Any line that is perpendicular to $\displaystyle 18-9y=13x$ must have a slope of what?

Possible Answers:

-13/9 $\displaystyle -13/9$

1/2 $\displaystyle 1/2$

13/9 $\displaystyle 13/9$

9/13 $\displaystyle 9/13$

-9/13 $\displaystyle -9/13$

Correct answer:

9/13 $\displaystyle 9/13$

Explanation:

Two lines are perpendicular if and only if their slopes are negative reciprocals of each other. To find the slope, we must put the equation into slope-intercept form, y=mx+b $\displaystyle y=mx+b$, where $\displaystyle m$ equals the slope of the line. First, we must subtract $\displaystyle 18$ from both sides of the equation, giving us $\displaystyle -9y=13x-18$. Next, we must divide both sides by $\displaystyle -9$, giving us $\displaystyle y=-13x/9+2$. We can now see that the slope of this line is -13/9 $\displaystyle -13/9$. Therefore, any line that is perpendicular to this one must have a slope of 9/13 $\displaystyle 9/13$.

Report an Error

Example Question #1 : How To Find The Slope Of A Perpendicular Line

What is the slope of any line perpendicular to $y=-\frac{1}{2}x+5$ $\displaystyle y=-\frac{1}{2}x+5$?

Possible Answers:

$\displaystyle 2$

$\displaystyle -2$

$\displaystyle 5$

$-\frac{1}{2}$ $\displaystyle -\frac{1}{2}$

$\frac{1}{2}$ $\displaystyle \frac{1}{2}$

Correct answer:

$\displaystyle 2$

Explanation:

The slope of a perpendicular line is the negative reciprocal of the original slope.

The original slope is $-\frac{1}{2}$ $\displaystyle -\frac{1}{2}$.

The negative reciprocal of the original slope is:

$-\frac{1}{-(\frac{1}{2})} = 2$ $\displaystyle -\frac{1}{-(\frac{1}{2})} = 2$

Report an Error

Example Question #2 : How To Find The Slope Of A Perpendicular Line

What is the slope of a line perpendicular to x=100 $\displaystyle x=100$?

Possible Answers:

$\displaystyle 0$

$\frac{1}{100}$ $\displaystyle \frac{1}{100}$

$\displaystyle -100$

$-\frac{1}{100}$ $\displaystyle -\frac{1}{100}$

100 $\displaystyle 100$

Correct answer:

$\displaystyle 0$

Explanation:

The equation x=100 $\displaystyle x=100$ is a vertical line on the coordinate plane. Any line perpendicular to a vertical line is a horizontal line. Horizontal lines have slopes of zero.

The correct answer is $\displaystyle 0$.

Report an Error

Example Question #1 : How To Find The Slope Of A Perpendicular Line

Assume the points (1,1) $\displaystyle (1,1)$ and (2,3) $\displaystyle (2,3)$ form a line. A perpendicular line is drawn to intersect this line. What is the slope of the perpendicular line?

Possible Answers:

$\frac{1}{2}$ $\displaystyle \frac{1}{2}$

$-\frac{1}{2}$ $\displaystyle -\frac{1}{2}$

$\displaystyle -2$

$\displaystyle 2$

$\displaystyle -1$

Correct answer:

$-\frac{1}{2}$ $\displaystyle -\frac{1}{2}$

Explanation:

Write the slope formula and find the slope of the first line.

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-1}{2-1}=\frac{2}{1}=2$ $\displaystyle m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-1}{2-1}=\frac{2}{1}=2$

The slope of the perpendicular line is the negative reciprocal of the original slope.

$-\frac{1}{(2)} =-\frac{1}{2}$ $\displaystyle -\frac{1}{(2)} =-\frac{1}{2}$

Therefore, the slope of the perpendicular line is $-\frac{1}{2}$ $\displaystyle -\frac{1}{2}$.

Report an Error

Example Question #3 : How To Find The Slope Of A Perpendicular Line

A line goes through the following (4,5) $\displaystyle (4,5)$ and (10,8) $\displaystyle (10,8)$.

Find the slope of a line perpendicular to the line given.

Possible Answers:

$\displaystyle -2$

$\displaystyle 2$

1.5 $\displaystyle 1.5$

0.5 $\displaystyle 0.5$

-0.5 $\displaystyle -0.5$

Correct answer:

$\displaystyle -2$

Explanation:

The slope of a line perpendicular is the negative reciprocal of the given line.

Since the given slope is calculated as $\frac{8-5}{10-4}=\frac{3}{6}=\frac{1}{2}$ $\displaystyle \frac{8-5}{10-4}=\frac{3}{6}=\frac{1}{2}$, then the slope of the perpendicular line would be (-)2=-2 $\displaystyle (-)2=-2$.

Report an Error

View Tutors

Godswill
Certified Tutor

Rivers State University, Bachelor of Engineering, Mechanical Engineering. Texas Southern University, Master of Science, Compu...

View Tutors

Adesuwa
Certified Tutor

Western Governors University, Bachelor's (in progress), Nursing.

View Tutors

Harrison
Certified Tutor

Hamilton College, Bachelor in Arts, Mathematics. University of Connecticut, Master of Science, Applied Mathematics.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Philadelphia, Calculus Tutors in Los Angeles, Reading Tutors in Seattle, SAT Tutors in Atlanta, Computer Science Tutors in San Francisco-Bay Area, GRE Tutors in San Francisco-Bay Area, Math Tutors in New York City, Algebra Tutors in San Diego, GMAT Tutors in Atlanta, MCAT Tutors in Washington DC

Popular Courses & Classes

MCAT Courses & Classes in Boston, SAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Denver, GRE Courses & Classes in Los Angeles, GMAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Phoenix, GMAT Courses & Classes in San Diego, Spanish Courses & Classes in Seattle, GRE Courses & Classes in Seattle, GMAT Courses & Classes in Washington DC

Popular Test Prep

GMAT Test Prep in San Francisco-Bay Area, ACT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Chicago, LSAT Test Prep in Denver, MCAT Test Prep in Atlanta, ISEE Test Prep in Dallas Fort Worth, MCAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Chicago, ACT Test Prep in Phoenix, SAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : How to find the slope of a perpendicular line

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #1 : Perpendicular Lines

Example Question #1 : How To Find The Slope Of A Perpendicular Line

Example Question #2 : How To Find The Slope Of A Perpendicular Line

Example Question #1 : How To Find The Slope Of A Perpendicular Line

Example Question #3 : How To Find The Slope Of A Perpendicular Line

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: