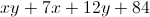Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : How to find the length of the side of a parallelogram

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #203 : Quadrilaterals

Find the perimeter of the following box in inches:

Geo_box

Possible Answers:

84xy $\displaystyle 84xy$

$\displaystyle x + y + 19$

$\displaystyle xy + 7x + 12y +84$

12x +7y $\displaystyle 12x +7y$

$\displaystyle 2x + 2y + 38$

Correct answer:

$\displaystyle 2x + 2y + 38$

Explanation:

The answer is $\displaystyle 2x + 2y + 38$.

You can find the perimeter by adding all of its respective sides as such:

$\displaystyle (12 + x) + (12 + x) + (7 + y) + (7 + y)$.

Adding like terms will result in

$\displaystyle 2x + 2y + 38$

If you chose $\displaystyle xy + 7x + 12y +84$, you multiplied the two sides to find the area.

If you chose $\displaystyle x + y + 19$, you only added two sides. Perimeter involves all 4 sides; so double the width and length.

Just remember, the width is 12 added to $\displaystyle x$. Not 12 times the side of $\displaystyle x$.

Report an Error

Example Question #208 : Quadrilaterals

A parallelogram has an area of $54\:cm^2$ $\displaystyle 54\:cm^2$. If the height is $6\:cm$ $\displaystyle 6\:cm$, what is the length of the base?

Possible Answers:

$9\:cm$ $\displaystyle 9\:cm$

$4.5\:cm$ $\displaystyle 4.5\:cm$

$18\:cm$ $\displaystyle 18\:cm$

$12\:cm$ $\displaystyle 12\:cm$

Cannot be determined

Correct answer:

$9\:cm$ $\displaystyle 9\:cm$

Explanation:

If the area of a parallelogram is given as $54\:cm^2$ $\displaystyle 54\:cm^2$ with a height of $6\:cm$ $\displaystyle 6\:cm$, we can refer back to the equation for the area of a parallelogram:

$A= b \cdot h$ $\displaystyle A= b \cdot h$, where $\displaystyle h$ is height and $\displaystyle b$ is the length of the base.

This very quickly becomes a problem of substituting in values and finding the value of an unknown variable, in this case, $\displaystyle b$:

$54\:cm^2=6\:cm \cdot b$ $\displaystyle 54\:cm^2=6\:cm \cdot b$

$\frac{54\:cm^2}{6\:cm}=b$ $\displaystyle \frac{54\:cm^2}{6\:cm}=b$

$b=9\:cm$ $\displaystyle b=9\:cm$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Parallelogram

A parallelogram has a base of 10in $\displaystyle 10in$ and an area of 35in^2 $\displaystyle 35in^2$. What is the height of the parallelogram?

Possible Answers:

1.25in $\displaystyle 1.25in$

3.5in $\displaystyle 3.5in$

3in $\displaystyle 3in$

3.25in $\displaystyle 3.25in$

Correct answer:

3.5in $\displaystyle 3.5in$

Explanation:

In order to find the height of this parallelogram apply the formula: $A=base\times height$ $\displaystyle A=base\times height$

$35=10\times height$ $\displaystyle 35=10\times height$

$height= \frac{35}{10}=3.5$ $\displaystyle height= \frac{35}{10}=3.5$

Report an Error

Example Question #210 : Quadrilaterals

A parallelogram has a height of 12ft $\displaystyle 12ft$ and an area of 168ft^2 $\displaystyle 168ft^2$. What is the length of the base of the parallelogram?

Possible Answers:

15ft $\displaystyle 15ft$

12ft $\displaystyle 12ft$

14ft $\displaystyle 14ft$

10ft $\displaystyle 10ft$

Correct answer:

14ft $\displaystyle 14ft$

Explanation:

To find the missing side of this parallelgram apply the formula: $A=base\times height$ $\displaystyle A=base\times height$

Thus, the solution is:

$168=12\times base$ $\displaystyle 168=12\times base$

$base=\frac{168}{12}=14$ $\displaystyle base=\frac{168}{12}=14$

Report an Error

Example Question #211 : Quadrilaterals

Given that a parallelogram has a height of 2.5ft $\displaystyle 2.5ft$ and an area of 20ft^2 $\displaystyle 20ft^2$. Find the base of the parallelogram.

Possible Answers:

12ft $\displaystyle 12ft$

6.5ft $\displaystyle 6.5ft$

8ft $\displaystyle 8ft$

7.5ft $\displaystyle 7.5ft$

Correct answer:

8ft $\displaystyle 8ft$

Explanation:

In order to find the base of this parallelogram apply the formula: $Area=base\times height$ $\displaystyle Area=base\times height$

Thus, the solution is:

$20=base\times2.5$ $\displaystyle 20=base\times2.5$

$base=\frac{20}{2.5}$ $\displaystyle base=\frac{20}{2.5}$

base=8 $\displaystyle base=8$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Parallelogram

Given: Quadrilateral ABCD $\displaystyle ABCD$ with diagonal $\overline{AC}$ $\displaystyle \overline{AC}$; $\bigtriangleup ABC \cong \bigtriangleup CDA$ $\displaystyle \bigtriangleup ABC \cong \bigtriangleup CDA$.

True or false: From the information given, it follows that Quadrilateral ABCD $\displaystyle ABCD$ is a parallelogram.

Possible Answers:

False

True

Correct answer:

True

Explanation:

Corresponding parts of congruent triangles are, by definition, congruent. Thus, from the statement $\bigtriangleup ABC \cong \bigtriangleup CDA$ $\displaystyle \bigtriangleup ABC \cong \bigtriangleup CDA$, it follows that:

$\overline{AB} \cong \overline{CD}$ $\displaystyle \overline{AB} \cong \overline{CD}$ and $\overline{BC} \cong \overline{DA}$ $\displaystyle \overline{BC} \cong \overline{DA}$

Quadrilateral ABCD $\displaystyle ABCD$ therefore has two sets of congruent opposite sides. This is a sufficient condition for the quadrilateral to be a parallelogram.

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Parallelogram

Quadrilateral ABCD $\displaystyle ABCD$ is both a rhombus and a rectangle.

True or false: Quadrilateral ABCD $\displaystyle ABCD$ must be a square.

Possible Answers:

True

False

Correct answer:

True

Explanation:

A rhombus is defined to be a parallelogram with four congruent sides; a rectangle is defined to be a parallelogram with four right angles.

A square is defined to be a parallelogram with four congruent sides and four right angles. If a parallelogram is both a rhombus and a rectangle, then it fits both characteristics and is therefore a square.

Report an Error

View Tutors

Christy
Certified Tutor

York University, Bachelor in Arts, Psychology.

View Tutors

Duaa
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Political Science and Government.

View Tutors

Aaron
Certified Tutor

Georgia Institute of Technology-Main Campus, Bachelor of Science, Biomedical Engineering.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Phoenix, LSAT Tutors in Washington DC, Computer Science Tutors in San Diego, Chemistry Tutors in New York City, Math Tutors in Phoenix, ACT Tutors in Denver, ISEE Tutors in Chicago, Spanish Tutors in San Francisco-Bay Area, GRE Tutors in Denver, French Tutors in Miami

Popular Courses & Classes

SSAT Courses & Classes in Seattle, GRE Courses & Classes in San Diego, GMAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Houston, MCAT Courses & Classes in Houston, ACT Courses & Classes in Boston, ISEE Courses & Classes in Phoenix, SAT Courses & Classes in Washington DC, GMAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Dallas Fort Worth

Popular Test Prep

GMAT Test Prep in Los Angeles, GRE Test Prep in Los Angeles, GRE Test Prep in Phoenix, ISEE Test Prep in Seattle, GMAT Test Prep in Philadelphia, ISEE Test Prep in Denver, GMAT Test Prep in San Diego, SAT Test Prep in Miami, SAT Test Prep in Houston, LSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : How to find the length of the side of a parallelogram

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #203 : Quadrilaterals

Example Question #208 : Quadrilaterals

Example Question #1 : How To Find The Length Of The Side Of A Parallelogram

Example Question #210 : Quadrilaterals

Example Question #211 : Quadrilaterals

Example Question #1 : How To Find The Length Of The Side Of A Parallelogram

Example Question #2 : How To Find The Length Of The Side Of A Parallelogram

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: