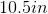All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find The Length Of The Side Of A Kite
The diagonals of a kite are 


We would do best to begin with a picture.

One of our diagonals is bisected by the other, and thus each half is 12. The other important thing to recall is that the diagonals of a kite are perpendicular. Therefore we have four right triangles. We can then use the Pythagorean Theorem to calculate the upper portion of the vertical diagonal to be 5. That means that the bottom portion of our diagonal is 9.

Using the Pythagorean Theorem, we can calculate our remaining sides to be 15.
Example Question #2 : How To Find The Length Of The Side Of A Kite
A kite has a perimeter of 

To find the missing side of this kite, work backwards using the formula:


The solution is:
Example Question #311 : Plane Geometry
A kite has a perimeter of 







To find the missing side of this kite, work backwards using the formula:


The solution is:
Example Question #4 : How To Find The Length Of The Side Of A Kite
A kite has a perimeter of 

To find the missing side of this kite, work backwards using the formula:


The solution is:
Example Question #5 : How To Find The Length Of The Side Of A Kite

Using the kite shown above, find the length of side


To find the missing side of this kite, work backwards using the formula:


The solution is:
Example Question #6 : How To Find The Length Of The Side Of A Kite

Using the kite shown above, find the length of side 

To find the missing side of this kite, work backwards using the formula:


The solution is:
Example Question #7 : How To Find The Length Of The Side Of A Kite
Ms. Dunn has a kite shaped backyard with a perimeter of 

To find the missing side of this kite, work backwards using the formula:


The solution is:
Example Question #8 : How To Find The Length Of The Side Of A Kite
A kite has a perimeter of 







To find the missing side of this kite, work backwards using the formula:


The solution is:
Example Question #9 : How To Find The Length Of The Side Of A Kite
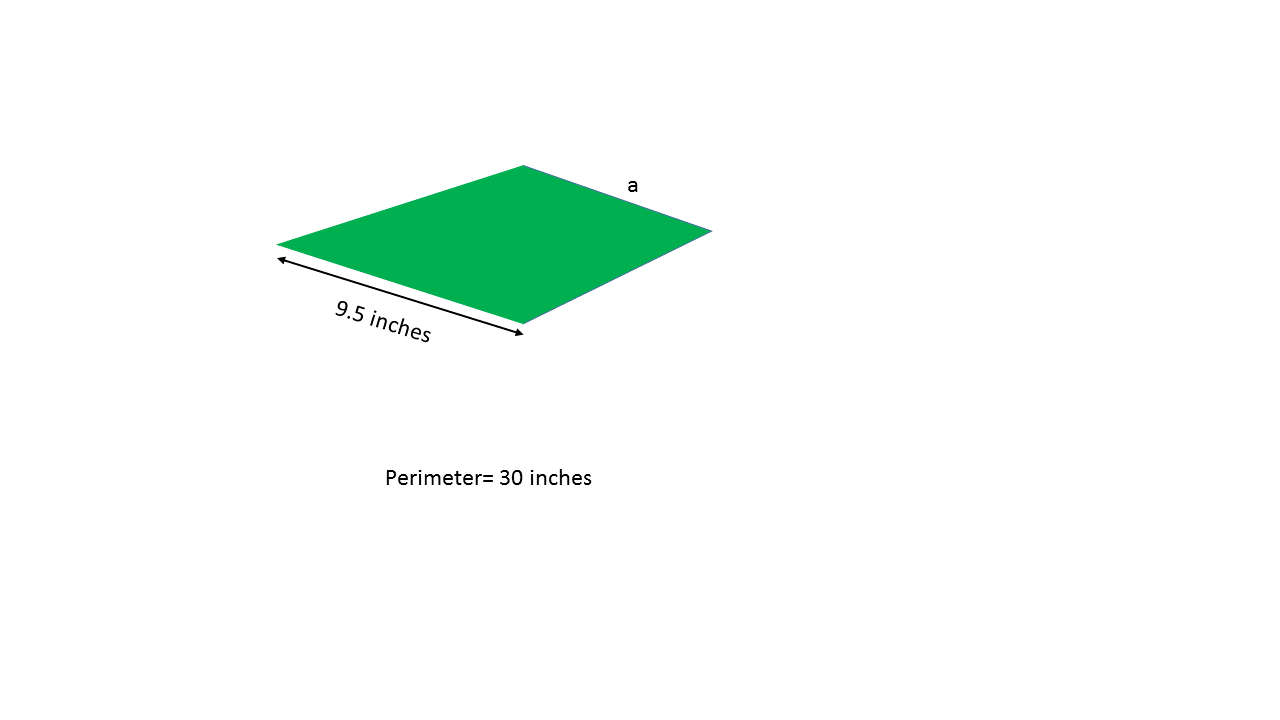
Using the above kite, find the length of side 
To find the missing side of this kite, work backwards using the formula:


The solution is:
Example Question #10 : How To Find The Length Of The Side Of A Kite
The lengths of the non-adjacent sides of a kite have the ratio 






The sides have the ratio 

Since the longer sides are 
Certified Tutor
Certified Tutor
All Intermediate Geometry Resources