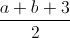We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Concepts

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 … 144 145 146 147 148 149 150 151 152 153 154 Next →

Example Question #2061 : Hspt Mathematics

What is the total degrees of the angles in a square?

Possible Answers:

270

180

360

Correct answer:

360

Explanation:

A square has four right angles which each have degrees.

To get the total you just multiple the measure of one by to get

90*4=360 .

Report an Error

Example Question #12 : Geometry

Angle $\angle ABC$ measures $20^{\circ}$

$\overrightarrow{BD}$ is the bisector of $\angle ABC$

$\overrightarrow{BE}$ is the bisector of $\angle CBD$

What is the measure of $\angle ABE$ ?

Possible Answers:

$5^{\circ}$

$15^{\circ}$

$40^{\circ}$

$10^{\circ}$

$30^{\circ}$

Correct answer:

$15^{\circ}$

Explanation:

Angle pic

Let's begin by observing the larger angle. $\angle ABC$ is cut into two 10-degree angles by $\overrightarrow{BD}$ . This means that angles $\angle ABD$ and $\angle CBD$ equal 10 degrees. Next, we are told that $\overrightarrow{BE}$ bisects $\angle CBD$ , which creates two 5-degree angles. $\angle ABE$ consists of $\angle ABD$ , which is 10 degrees, and $\angle DBE$ , which is 5 degrees. We need to add the two angles together to solve the problem.

$\angle ABE=\angle ABD+\angle DBE$

$\angle ABE=10^{\circ}+5^{\circ}$

$\angle ABE=15^{\circ}$

Report an Error

Example Question #2061 : Hspt Mathematics

If $\overleftrightarrow{FH} \parallel \overleftrightarrow{AD}$ , $\overline{BE}\perp \overleftrightarrow{GC}$ , and $m\angle HGC=58^\circ$ , what is the measure, in degrees, of $\angle ABE$ ?

Alternate interior angles

Possible Answers:

122

148

Correct answer:

148

Explanation:

The question states that $\overleftrightarrow{FH} \parallel \overleftrightarrow{AD}$ . The alternate interior angle theorem states that if two parallel lines are cut by a transversal, then pairs of alternate interior angles are congruent; therefore, we know the following measure:

$m\angle GCA = 58^\circ$

The sum of angles of a triangle is equal to 180 degrees. The question states that $\overline{BE}\perp \overleftrightarrow{GC}$ ; therefore we know the following measure:

$m \angle BEC = 90^\circ$

Use this information to solve for the missing angle: $\angle EBC$

$180^\circ=m\angle EBC+58^\circ+90^\circ$

$m\angle EBC=32^\circ$

The degree measure of a straight line is 180 degrees; therefore, we can write the following equation:

$180^\circ=m\angle ABE+32^\circ$

$m\angle ABE=148^\circ$

The measure of $\angle ABE$ is 148 degrees.

Report an Error

Example Question #2061 : Hspt Mathematics

What is the slope of a line through the points (2,5) and (-2,3) ?

Possible Answers:

$-\frac{1}{2}$

$\frac{1}{2}$

Undefined slope

Correct answer:

$\frac{1}{2}$

Explanation:

Use the slope fomula, setting $x_{1} = -2, x_{2} = 2,y_{1} = 3, y_{2} = 5$

$m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{5-3}{2-(-2)} = \frac{2}{4} =\frac{1}{2}$

Report an Error

Example Question #2062 : Hspt Mathematics

In which quadrant, or on which axis, is the point with coordinates (6,-6) located?

Possible Answers:

Quadrant IV

Quadrant III

Quadrant II

The -axis

Quadrant I

Correct answer:

Quadrant IV

Explanation:

Any point with a positive -coordinate and a negative -coordinate is located in the lower right quadrant - Quadrant IV.

Report an Error

Example Question #1474 : Concepts

Which of the following is an equation of a line with slope 0?

Possible Answers:

y = x+7

y = -5

x = 6

$y=x^{2} +1$

x+y= 10

Correct answer:

y = -5

Explanation:

A line with slope 0 has equation y = b for some real value .

Report an Error

Example Question #2071 : Hspt Mathematics

Axes

Give the equation of the red line in slope-intercept form.

Possible Answers:

$y = -\frac{4}{7}x + 6$

$y = \frac{4}{7}x + 6$

$y =- \frac{7}{4}\left (x + 6 \right )$

$y = \frac{7}{4}x + 6$

$y =- \frac{7}{4}x + 6$

Correct answer:

$y = \frac{7}{4}x + 6$

Explanation:

The slope of the line is

$m = \frac{y_{2}- y_{1}}{x_{2}- x_{1}} = \frac{6- (-1)}{0-(-4)} = \frac{7}{4}$

The -intercept of the line has -coordinate b= 6

The slope-intercept form can be written:

y = mx+b

Replace:

$y = \frac{7}{4}x+6$

Report an Error

Example Question #2071 : Hspt Mathematics

Axes_2

The green and blue lines are perpendicular: What is the slope of the blue line?

Possible Answers:

$\frac{1}{3}$

It cannot be determined from the information given.

$-\frac{1}{3}$

Correct answer:

Explanation:

The slope of the blue line, being perpendicular to the green line, is the opposite of the reciprocal of the slope of the green line. The slope of the green line can be found using the slope formula:

$m = \frac{y_{2}- y_{1}}{x_{2}- x_{1}} = \frac{10-0}{0-30} = -\frac{1}{3}$

The opposite of the reciprocal of $-\frac{1}{3}$ is 3, and this is the slope of the blue line.

Report an Error

Example Question #1 : How To Find The Midpoint Of A Line Segment

A line segment on the coordinate plane has endpoints (a-5,-b) and (b+8, a-4) . In terms of and , as applicable, give the -coordinate of its midpoint.

Possible Answers:

$\frac{a + b + 3}{2}$

a - b - 4

a + b + 3

$\frac{a - b - 4}{2}$

$\frac{a - b - 13}{2}$

Correct answer:

$\frac{a + b + 3}{2}$

Explanation:

The -coordinate of the midpoint of a line segment is the mean of the -coordinates of its endpoints. Therefore, the -coordinate is

$x= \frac{(a-5)+(b+8)}{2} = \frac{a+b-5+8}{2} = \frac{a+b+3}{2}$ .

Report an Error

Example Question #1 : Midpoint Formula

A line segment on the coordinate plane has endpoints (a-5,-b) and (b+8, a-4) . In terms of and , as applicable, give the -coordinate of its midpoint.

Possible Answers:

$\frac{a + b + 3}{2}$

$\frac{a + b - 4}{2}$

a + b + 3

$\frac{a - b - 4}{2}$

a - b - 4

Correct answer:

$\frac{a - b - 4}{2}$

Explanation:

The -coordinate of the midpoint of a line segment is the mean of the -coordinates of its endpoints. Therefore, the -coordinate is

$y= \frac{(a-4)+(-b)}{2} = \frac{a-b-4}{2}$ .

Report an Error

← Previous 1 2 … 144 145 146 147 148 149 150 151 152 153 154 Next →

View Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

View Tutors

Aaron
Certified Tutor

Portland State University, Bachelors, Economics. Portland State University, Masters, Environmental and Resource Management.

View Tutors

Chase
Certified Tutor

Western Governors University, Bachelor of Science, Mathematics.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Denver, Algebra Tutors in San Diego, Chemistry Tutors in Boston, Math Tutors in New York City, ISEE Tutors in Seattle, Algebra Tutors in Miami, MCAT Tutors in New York City, Spanish Tutors in Washington DC, ISEE Tutors in Denver, GRE Tutors in Washington DC

Popular Courses & Classes

SAT Courses & Classes in Philadelphia, GRE Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Los Angeles, GRE Courses & Classes in New York City, MCAT Courses & Classes in Houston, ACT Courses & Classes in Miami, SSAT Courses & Classes in Houston, SSAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Chicago, GMAT Courses & Classes in Denver

Popular Test Prep

ACT Test Prep in Los Angeles, MCAT Test Prep in Philadelphia, MCAT Test Prep in Los Angeles, LSAT Test Prep in Atlanta, ISEE Test Prep in San Francisco-Bay Area, GMAT Test Prep in Denver, ACT Test Prep in Miami, MCAT Test Prep in Houston, SAT Test Prep in Miami, MCAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Concepts

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #2061 : Hspt Mathematics

Example Question #12 : Geometry

Example Question #2061 : Hspt Mathematics

Example Question #2061 : Hspt Mathematics

Example Question #2062 : Hspt Mathematics

Example Question #1474 : Concepts

Example Question #2071 : Hspt Mathematics

Example Question #2071 : Hspt Mathematics

Example Question #1 : How To Find The Midpoint Of A Line Segment

Example Question #1 : Midpoint Formula

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: