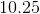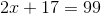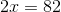In order to solve for the variable, \(\displaystyle x\), we need to isolate it on the left side of the equation. We will do this by reversing the operations done to the variable by performing the opposite of each operation on both sides of the equation. 

Let's begin by rewriting the given equation.

\(\displaystyle \frac{x}{4}+11=15\)

Subtract \(\displaystyle 11\) from both sides of the equation.

\(\displaystyle \frac{x}{4}+11-11=15-11\)

Simplify.

\(\displaystyle \frac{x}{4}=4\)

Multiply both sides of the equation by \(\displaystyle 4\).

\(\displaystyle \frac{x}{4}\times 4=4\times 4\)

Solve.

\(\displaystyle x=16\)

\(\displaystyle \left | -4x + 13 \right | \ge 9\) can be rewritten as the compound inequality

\(\displaystyle -4x + 13 \le - 9 \textup{ or } -4x + 13 \ge 9\).

The solution set will be the union of the two individual solution sets. Find the solution set of the first inequality as follows:

Isolate \(\displaystyle x\) by first subtracting \(\displaystyle -13\) from both sides:

\(\displaystyle -4x + 13 \le - 9\)

\(\displaystyle -4x + 13- 13 \le - 9 - 13\)

\(\displaystyle -4x \le -22\)

Divide both sides by \(\displaystyle -4\), reversing the direction of the inequality symbol, since you are dividing by a negative number:

\(\displaystyle -4x \div (-4){ \color{Red} \ge} -22 \div (-4)\)

\(\displaystyle x \ge 5\frac{1}{2}\).

In interval notation, this is the set \(\displaystyle \left [ 5 \frac{1}{2} , \infty \right )\).

Find the solution set of the other inequality similarly:

\(\displaystyle -4x + 13 \ge 9\)

\(\displaystyle -4x + 13 - 13 \ge 9 - 13\)

\(\displaystyle -4x \ge -4\)

\(\displaystyle -4x \div (-4) \le -4 \div (-4)\)

\(\displaystyle x \le 1\)

In interval notation, this is the set \(\displaystyle \left ( -\infty, 1 \right ]\).

The union of these sets is the solution set: \(\displaystyle \left ( -\infty, 1 \right ] \cup \left [ 5 \frac{1}{2} , \infty \right )\).

Solve for \(\displaystyle x\) in the equation

\(\displaystyle 2x+ 17 = 99\)

by isolating \(\displaystyle x\) on the left side. Do this by reversing the operations in the reverse of the order of operations.

First, subtract 17 from both sides:

\(\displaystyle 2x+ 17 -17 = 99 - 17\)

\(\displaystyle 2x= 82\)

Now, divide both sides by 2:

\(\displaystyle 2x \div 2 = 82 \div 2\)

\(\displaystyle x = 41\)

One way to find 25% of this value is to multiply 41 by 25 and divide by 100:

\(\displaystyle \frac{41 \times 25}{100} = \frac{1,025}{100} = 10.25\),

the correct choice.

Given a quadratic function

\(\displaystyle f(x)=ax^2 +bx+c\)

the vertex will always be

\(\displaystyle (-\frac{b}{2a},\frac{4ac-b^2}{4a})\).

Thus, since our function is 

\(\displaystyle f(x) = 2x^2 - 3x + 17\)

\(\displaystyle a=2\), \(\displaystyle b=-3\), and \(\displaystyle c=17\).

We plug these variables into the formula to get the vertex as

\(\displaystyle (-\frac{-3}{2\times2},\frac{4\times2\times17-(-3)^2}{4\times2})\)

\(\displaystyle (-\frac{-3}{4},\frac{136-9}{8})\)

\(\displaystyle =(\frac{3}{4},\frac{127}{8})\).

Hence, the vertex of

\(\displaystyle f(x) = 2x^2 - 3x + 17\)

is

\(\displaystyle (\frac{3}{4},\frac{127}{8})\).

The discriminant of a quadratic polynomial

\(\displaystyle f(x)=ax^2+bx+c\)

is given by

\(\displaystyle b^2-4ac\).

Thus, since our quadratic polynomial is 

\(\displaystyle f(x)=6x^2-3x+7\),

\(\displaystyle a=6\), \(\displaystyle b=-3\), and \(\displaystyle c=7\). 

Plugging these values into the discriminant equation, we find that the discriminant is

\(\displaystyle 9-4\times6\times7\).

A polynomial equation of the form

\(\displaystyle ax^{2}+bx+c = 0\)

has one and only one (real) solution if and only if its discriminant is equal to zero - that is, if its coefficients satisfy the equation

\(\displaystyle b^{2}-4ac = 0\)

In each of the choices, \(\displaystyle a = 4\) and \(\displaystyle c = 25\), so it suffices to determine the value of \(\displaystyle b\) which satisfies this equation. Substituting, we get

\(\displaystyle b^{2}-4 (4)(25) = 0\)

\(\displaystyle b^{2}-400 = 0\)

Solve for \(\displaystyle b\) by first adding 400 to both sides:

\(\displaystyle b^{2}-400 + 400 = 0 + 400\)

\(\displaystyle b^{2} = 400\)

Take the square root of both sides:

\(\displaystyle b =\pm \sqrt{400} = \pm 20\)

The choice that matches this value of \(\displaystyle b\) is the equation

\(\displaystyle 4x^{2}+ 20x + 25 = 0\)

To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form 

\(\displaystyle ax^{2}+bx+c = 0\)

To accomplish this, first, multiply the binomials on the left using the FOIL technique:

\(\displaystyle (2x-5)(x+4) = -6\)

\(\displaystyle 2x(x)+2x(4)-5(x)-5(4)= -6\)

\(\displaystyle 2x ^{2}+8x -5x-20= -6\)

Collect like terms:

\(\displaystyle 2x ^{2}+3x-20= -6\)

Add 6 to both sides:

\(\displaystyle 2x ^{2}+3x-20 + 6 = -6 + 6\)

\(\displaystyle 2x ^{2}+3x-14= 0\)

The key to determining the nature of the solution set is to examine the discriminant \(\displaystyle b^{2} - 4ac\). Setting \(\displaystyle a = 2, b = 3, c= -14\), the value of the discriminant is 

\(\displaystyle b^{2} - 4ac= 3^{2} -4(2)(-14) = 9 - (-112) = 9+112 = 121\)

The discriminant is a positive number; furthermore, it is a perfect square, being equal to the square of 11. Therefore, the solution set comprises two rational solutions.

A polynomial equation of the standard form

\(\displaystyle ax^{2}+bx+c = 0\)

has one and only one (real) solution if and only if its discriminant is equal to zero - that is, if its coefficients satisfy the equation

\(\displaystyle b^{2}-4ac = 0\)

Each of the choices can be rewritten in standard form by subtracting the term on the right from both sides. One of the choices can be rewritten as follows:

\(\displaystyle 9x^{2} + 25 =10x\)

\(\displaystyle 9x^{2} + 25 - 10x =10x - 10x\)

\(\displaystyle 9x^{2} - 10x + 25 =0\)

By similar reasoning, the other four choices can be written:

\(\displaystyle 9x^{2} - 20x + 25 =0\)

\(\displaystyle 9x^{2} - 30x + 25 =0\)

\(\displaystyle 9x^{2} - 40x + 25 =0\)

\(\displaystyle 9x^{2} - 50x + 25 =0\)

In each of the five standard forms, \(\displaystyle a= 9\) and \(\displaystyle c = 25\), so it is necessary to determine the value of \(\displaystyle b\) that produces a zero discriminant. Substituting accordingly:

\(\displaystyle b^{2}-4ac = 0\)

\(\displaystyle b^{2}-4(9)(25) = 0\)

\(\displaystyle b^{2}-900 = 0\)

Add 900 to both sides and take the square root:

\(\displaystyle b^{2}-900 + 900 = 0+ 900\)

\(\displaystyle b^{2}= 900\)

\(\displaystyle b = \pm \sqrt{900} = \pm 30\)

Of the five standard forms, 

\(\displaystyle 9x^{2} - 30x + 25 =0\)

fits this condition. This is the standard form of the equation 

\(\displaystyle 9x^{2} + 25 =30x\),

the correct choice.

To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form 

\(\displaystyle ax^{2}+bx+c = 0\)

This can be done by simply switching the first and second terms:

\(\displaystyle 6x+ 2x^{2}+ 7= 0\)

\(\displaystyle 2x^{2}+6x+ 7= 0\)

The key to determining the nature of the solution set is to examine the discriminant  \(\displaystyle b^{2} - 4ac\). Setting \(\displaystyle a = 2, b= 6, c= 7\), the value of the discriminant is 

\(\displaystyle b^{2} - 4ac =6^{2} - 4(2)(7) = 36-56=-20\)

The discriminant has a negative value. It follows that the solution set comprises two imaginary values.

To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form 

\(\displaystyle ax^{2}+bx+c = 0\)

This can be done by adding 17 to both sides:

\(\displaystyle 2x^{2}+ 5x+ 17 = -17+ 17\)

\(\displaystyle 2x^{2}+ 5x+ 17 = 0\)

The key to determining the nature of the solution set is to examine the discriminant 

\(\displaystyle b^{2} - 4ac\). Setting \(\displaystyle a = 2, b = 5, c= 17\), the value of the discriminant is 

\(\displaystyle 5^{2} - 4(2)(17) = 25 - 136 = -111\)

This value is negative. Consequently, the solution set comprises two imaginary numbers.