All High School Math Resources
Example Questions
Example Question #1 : Angles
The angles containing the variable 
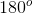
Because 
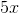
Example Question #1 : Understanding Complementary And Suplmentary Angles
Are 

Yes
Maybe
Not enough information
No
Yes
Complementary angles add up to 
Example Question #2 : Angles
What angle is complementary to 
Two complementary angles add up to 
Therefore, 
Example Question #3 : Angles
Which of the following angles is supplementary to 
When two angles are supplementary, they add up to 
For this problem, we can set up an equation and solve for the supplementary angle:
Example Question #4 : Angles
What angle is supplementary to 
Supplementary angles add up to 
Example Question #1 : Understanding Complementary And Suplmentary Angles
The angles are supplementary, therefore, the sum of the angles must equal 
Example Question #3 : Graphing Functions
Are 

Yes
Not enough information
No
Yes
Since supplementary angles must add up to 
Example Question #5 : Angles
Which of the following angles is complementary to 
Two complementary angles add up to 
Example Question #6 : Angles
What angle is supplementary to 
When two angles are supplementary, they add up to 
Solve for 
Example Question #3 : Angles
Which of the following angles is coterminal with 
For an angle to be coterminal with 









Certified Tutor
Certified Tutor
All High School Math Resources

 and
and  .
.


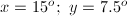

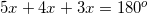





























 .
.



































![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{2\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99513/gif.latex)


![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{9\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99515/gif.latex)


![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{12\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99517/gif.latex)





