High School Math : Squares
Study concepts, example questions & explanations for High School Math
All High School Math Resources
Example Questions
Example Question #3 : How To Find The Area Of A Square
A half circle has an area of 
72
144
36
81
108
144
If the area of the half circle is 
Use the formula for the area of a circle to solve for the radius:
36π = πr2
r = 6
If the radius is 6, then the diameter is 12. We know that the sides of the square are the same length as the diameter, so each side has length 12.
Therefore the area of the square is 12 x 12 = 144.
Example Question #391 : Act Math
Eric has 160 feet of fence for a parking lot he manages. If he is using all of the fencing, what is the area of the lot assuming it is square?
The area of a square is equal to its length times its width, so we need to figure out how long each side of the parking lot is. Since a square has four sides we calculate each side by dividing its perimeter by four.
Each side of the square lot will use 40 feet of fence.
Example Question #1 : How To Find The Perimeter Of A Square
A circle with a radius 2 in is inscribed in a square. What is the perimeter of the square?
32 in
28 in
12 in
24 in
16 in
16 in
To inscribe means to draw inside a figure so as to touch in as many places as possible without overlapping. The circle is inside the square such that the diameter of the circle is the same as the side of the square, so the side is actually 4 in. The perimeter of the square = 4s = 4 * 4 = 16 in.
Example Question #21 : Squares
Square X has 3 times the area of Square Y. If the perimeter of Square Y is 24 ft, what is the area of Square X, in sq ft?
54
72
144
108
112
108
Find the area of Square Y, then calculate the area of Square X.
If the perimeter of Square Y is 24, then each side is 24/4, or 6.
A = 6 * 6 = 36 sq ft, for Square Y
If Square X has 3 times the area, then 3 * 36 = 108 sq ft.
Example Question #254 : Geometry
A square has an area of 
The area of the given square is given by 
Example Question #11 : Squares
A square garden has an area of 64 square feet. If you add 3 feet to each side, what is the new perimeter of the garden?
25
32
121
44
20
44
By finding the square root of the area of the garden, you find the length of one side, which is 8. We add 3 feet to this, giving us 11, then multiply this by 4 to get 44 feet for the perimeter.
Example Question #11 : Squares
The area of the shaded region of a square is 18. What is the perimeter of the square?
28
24
20
36
24
The area of the shaded region, which covers half of the square is 18 meaning that the total area of the square is 18 x 2, or 36. The area of a square is equal to the length of one side squared. Since the square root of 36 is 6, the length of 1 side is 6. The perimeter is the length of 1 side times 4 or 6 x 4.
Example Question #11 : Squares
The area of a square is 
The area of a square is given by 
Example Question #258 : Geometry
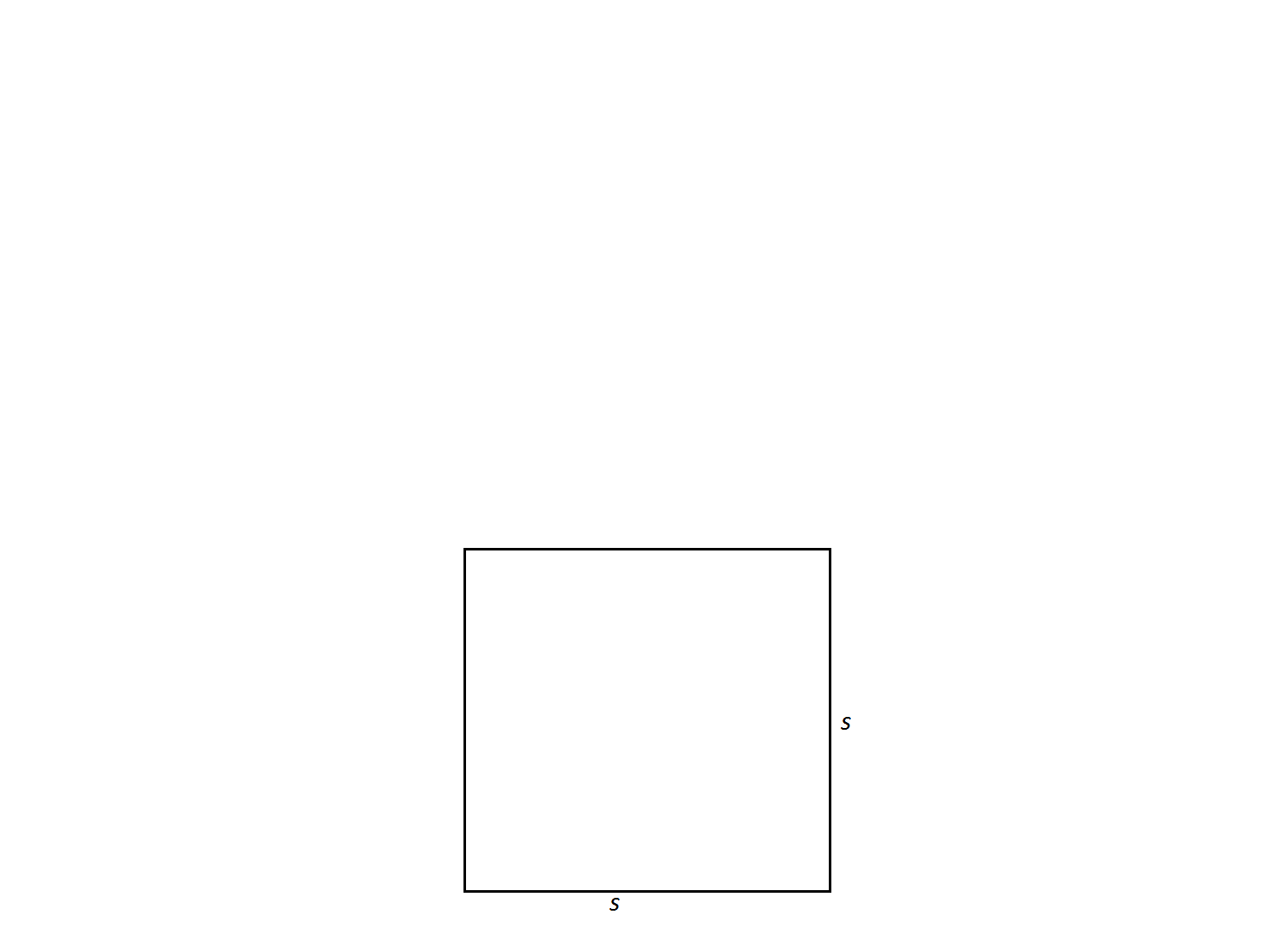
A square has a side length of 
Not enough information to solve
In order to find the perimeter of a square, one must add up all of its side lengths. The side lengths of a square are all equal; therefore, the formula for the perimeter of a square is 
Remember perimeter should be expressed in single units not units squared. Thus, 
Example Question #161 : Quadrilaterals
The diagonal of a square has a length of 10 inches. What is the perimeter of the square in inches squared?
Using the Pythagorean Theorem, we can find the edge of a side to be √50, by 2a2=102. This can be reduced to 5√2. This can then be multiplied by 4 to find the perimeter.
Certified Tutor
Certified Tutor
All High School Math Resources
