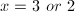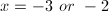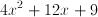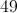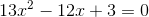We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Quadratic Equations and Inequalities

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 Next →

Example Question #1 : Simplifying And Expanding Quadratics

Solve the equation for .

$\small \frac{1}{x}=\frac{x+1}{6}$

Possible Answers:

$\small x=-3\ or\ 2$

$\small x=3\ or\ 2$

$\small x=3\ or\ -2$

$\small x=-3\ or\ -2$

Correct answer:

$\small x=-3\ or\ 2$

Explanation:

$\small \small \frac{1}{x}=\frac{x+1}{6}$

Cross multiply.

$\small 6=x(x+1)$

$\small 6=x^2+x$

Set the equation equal to zero.

$\small 0=x^2+x-6$

Factor to find the roots of the polynomial.

3*-2=-6 and 3+(-2)=1

$\small 0=(x+3)(x-2)$

$\small 0=x+3; x=-3$

$\small 0=x-2; x=2$

Report an Error

Example Question #1 : Foil

Evaluate $(2x+3)^{2}$

Possible Answers:

$4x^{2}+12x+9$

$\dpi{100} \dpi{100} 4x^{2}+9$

$\dpi{100} 4x+12$

$\dpi{100} 4x^{3}+12x^{2}+9x$

$\dpi{100} 4x^{2}+9x+9$

Correct answer:

$4x^{2}+12x+9$

Explanation:

In order to evaluate $(2x+3)^{2}$ one needs to multiply the expression by itself using the laws of FOIL. In the foil method, one multiplies in the following order: first terms, outer terms, inner terms, and last terms.

$\dpi{100} (2x+3)^{2}=(2x+3)(2x+3)$

Multiply terms by way of FOIL method.

=(2x*2x)+(2x*3)+(3*2x)+(3*3)

Now multiply and simplify.

$=4x^{2}+6x+6x+9$

$\rightarrow 4x^{2}+12x+9$

Report an Error

Example Question #11 : Quadratic Equations And Inequalities

Expand (x+7)(x-2) .

Possible Answers:

x^2+7x-2x-7

x^2+5x-14

x^2+9

x^2-5x-14

x^2-14x+5

Correct answer:

x^2+5x-14

Explanation:

To solve our given equation, we need to use FOIL (First, Outer, Inner, Last).

(x+7)(x-2)=x^2-2x+7x-14

Combine like terms.

(x+7)(x-2)=x^2+5x-14

Report an Error

Example Question #41 : Intermediate Single Variable Algebra

FOIL (x+1)(x-3) .

Possible Answers:

x^2+3x+4

$x^2+2x-\frac{1}{3}$

x^2-4x-3

$x^2+2x-\frac{2}{3}$

x^2-2x-3

Correct answer:

x^2-2x-3

Explanation:

Remember FOIL stands for First Outer Inner Last.

(x+1)(x-3)=x^2+1x-3x-3

Combine like terms to get x^2-2x-3 .

Report an Error

Example Question #1 : Understanding The Discriminant

Use the discriminant to determine the nature of the roots:

4x^2-40x+25=0

Possible Answers:

rational root

irrational roots

rational roots

imaginary roots

imaginary root

Correct answer:

irrational roots

Explanation:

The formula for the discriminant is:

b^2 - 4ac

=(-40)^2 - 4(4)(25)

$=1200^{}$

Since the discriminant is positive and not a perfect square, there are irrational roots.

Report an Error

Example Question #2 : Understanding The Discriminant

Use the discriminant to determine the nature of the roots:

2y^2+6y+5=0

Possible Answers:

imaginary root

rational roots

rational root

imaginary roots

irrational roots

Correct answer:

imaginary roots

Explanation:

The formula for the discriminant is:

b^2 - 4ac

=(6)^2 - 4(2)(5)

=-4

Since the discriminant is negative, there are imaginary roots.

Report an Error

Example Question #3 : Understanding The Discriminant

Use the discriminant to determine the nature of the roots:

4x^2-8x+13=0

Possible Answers:

imaginary root

imaginary roots

real roots

Cannot be determined

real root

Correct answer:

imaginary roots

Explanation:

The formula for the discriminant is:

b^2 - 4ac

=(-8)^2 - 4(4)(13)

=-144

Since the discriminant is negative, there are imaginary roots.

Report an Error

Example Question #1 : Discriminants

Given $2x^{2}+3x-5=0$ , what is the value of the discriminant?

Possible Answers:

Correct answer:

Explanation:

In general, the discriminant is $b^{2}-4ac$ .

In this particual case $a=2, b=3\; and\; c=-5$ .

Plug in these three values and simplify: $(3)^{2}-4(2)(-5)= 49$

Report an Error

Example Question #1 : Understanding Quadratic Roots

Write an equation with the given roots:

$\frac{3}{4}, \frac{1}{3}$

Possible Answers:

12x^2-13x+3=0

14x^2-13x+3=0

13x^2-12x+3=0

13x^2-12x+2=0

13x^2-13x+3=0

Correct answer:

12x^2-13x+3=0

Explanation:

To write an equation, find the sum and product of the roots. The sum is the negative coefficient of , and the product is the integer.

Sum: $(\frac{3}{4})+(\frac{1}{3})=\frac{13}{12}$

Product: $(\frac{3}{4})\cdot (\frac{1}{3})=\frac{1}{4}$

Subtract the sum and add the product.

The equation is:

$x^2 - \frac{13}{12}x+\frac{1}{4}=0$

Multiply the equation by :

12x^2+-13x+3=0

Report an Error

Example Question #1591 : High School Math

Write an equation with the given roots:

$2 \pm \sqrt{3}$

Possible Answers:

x^2-4x+1=0

x^2-4x+2=0

x^2-2x+2=0

x^2-3x+2=0

x^2-3x+1=0

Correct answer:

x^2-4x+1=0

Explanation:

To write an equation, find the sum and product of the roots. The sum is the negative coefficient of , and the product is the integer.

Sum: $(2 + \sqrt{3})+(2 - \sqrt{3})=4$

Product: $(2 + \sqrt{3})\cdot (2 - \sqrt{3})=4-3=1$

Subtract the sum and add the product.

The equation is:

x^2 -4x+1=0

Report an Error

← Previous 1 2 3 4 5 6 7 Next →

View Tutors

Saarim
Certified Tutor

St Edwards University, Bachelor of Science, Mathematics.

View Tutors

David
Certified Tutor

Rhode Island College, Bachelor in Arts, English. Rhode Island College, Masters in Education, English.

View Tutors

Justin
Certified Tutor

University of Washington-Seattle Campus, Current Undergrad Student, Biomedical Engineering.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in San Diego, Biology Tutors in Philadelphia, Biology Tutors in Phoenix, French Tutors in Phoenix, Math Tutors in San Francisco-Bay Area, Physics Tutors in Atlanta, Physics Tutors in Washington DC, GRE Tutors in Dallas Fort Worth, English Tutors in Seattle, ACT Tutors in Philadelphia

Popular Courses & Classes

SSAT Courses & Classes in Chicago, SSAT Courses & Classes in Los Angeles, SSAT Courses & Classes in New York City, MCAT Courses & Classes in Seattle, GRE Courses & Classes in Washington DC, ISEE Courses & Classes in Phoenix, MCAT Courses & Classes in Philadelphia, ISEE Courses & Classes in San Diego, Spanish Courses & Classes in Chicago, GMAT Courses & Classes in Miami

Popular Test Prep

GRE Test Prep in Los Angeles, SAT Test Prep in Atlanta, ISEE Test Prep in Phoenix, SAT Test Prep in San Diego, SAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Washington DC, MCAT Test Prep in Philadelphia, ISEE Test Prep in Seattle, ACT Test Prep in Houston, GRE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Quadratic Equations and Inequalities

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Simplifying And Expanding Quadratics

Example Question #1 : Foil

Example Question #11 : Quadratic Equations And Inequalities

Example Question #41 : Intermediate Single Variable Algebra

Example Question #1 : Understanding The Discriminant

Example Question #2 : Understanding The Discriminant

Example Question #3 : Understanding The Discriminant

Example Question #1 : Discriminants

Example Question #1 : Understanding Quadratic Roots

Example Question #1591 : High School Math

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: