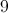High School Math : How to find the length of the diagonal of a hexagon
Study concepts, example questions & explanations for High School Math
All High School Math Resources
Example Questions
Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon
What is the length of a diagonal of a regular hexagon with side length 
Regular hexagons are comprised of six equilateral triangles; in our question, these triangles each have side length 4 (see diagram).
The length of a diagonal is equal to two times the length of the side. In this instance, the answer is 8.
Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon
How many diagonals are there in a regular hexagon?
A diagonal is a line segment joining two non-adjacent vertices of a polygon. A regular hexagon has six sides and six vertices. One vertex has three diagonals, so a hexagon would have three diagonals times six vertices, or 18 diagonals. Divide this number by 2 to account for duplicate diagonals between two vertices. The formula for the number of vertices in a polygon is:
where 
Example Question #2 : How To Find The Length Of The Diagonal Of A Hexagon
How many diagonals are there in a regular hexagon?
18
3
6
9
10
9
A diagonal connects two non-consecutive vertices of a polygon. A hexagon has six sides. There are 3 diagonals from a single vertex, and there are 6 vertices on a hexagon, which suggests there would be 18 diagonals in a hexagon. However, we must divide by two as half of the diagonals are common to the same vertices. Thus there are 9 unique diagonals in a hexagon. The formula for the number of diagonals of a polygon is:
where n = the number of sides in the polygon.
Thus a pentagon thas 5 diagonals. An octagon has 20 diagonals.
All High School Math Resources
