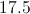To find the area of a kite using diagonals you use the following equation  

That diagonals ( and )are the lines created by connecting the two sides opposite of each other.

Plug in the diagonals for  and  to get 

Then multiply and divide to get the area. 

The answer is 

The formula for the area of a kite is:

Where  is the length of one diagonal and  is the length of the other diagonal

Plugging in our values, we get:

The formula for the area of a kite is:

where  is the length of one diagonal and  is the length of another diagonal.

Use the formulas for a  triangle and a  triangle to find the lengths of the diagonals. The formula for a  triangle is  and the formula for a  triangle is .

Our  triangle is: 

Our  triangle is: 

Plugging in our values, we get:

To solve for  we must get all of the numbers on the other side of the equation as .

To do this in a problem where a number is being added to , we must subtract the number from both sides of the equation.

In this case the number is  so we subtract  from each side of the equation to make it look like this 

The numbers on the left side cancel to leave  by itself.

To do the necessary subtraction we need to know how to subtract decimals from each other.

To subtract decimals you place the first decimal over the top of the other aligned by the decimal point. 

Then go through each place and subtract the top number by the bottom number.

Subtract the numbers in each place like you would any number  and

Combine the numbers and keep the decimal in the same place to get 

The answer is 

To solve for  we must get all of the numbers on the other side of the equation of .

To do this in a problem where  is being multiplied by a number, we must divide both sides of the equation by the number.

In this case the number is  so we divide each side of the equation by  to make it look like this 

Then we must divide the decimals by each other to find the answer.

To divide decimals we line the decimals up like this .

Then ignoring all of the decimal places we divide the top number by the bottom number to get 

Then we must apply the decimals.

However many decimal places there are in the denominator will be subtracted from the number of decimal places in the numerator to get the final number of decimal places in our answer.

If the number is positive we move the decimal that number of places to the left of our number.

If the number is negative we move the decimal that number of places to the right of our number.

In this case it would be  so we don't have any decimal places and the answer is  .

To solve for  we must get all of the numbers on the other side of the equation of .

To do this in a problem where  is being subtracted by a number, we must add the number to both sides of the equation.

In this case the number is  so we add  to each side of the equation to make it look like this 

The numbers on the left side cancel to leave  by itself.

Then we must perform the necessary addition to get the answer.

To add decimals together you place the decimals one over the top of the other aligned by the decimal point.

If there are no numbers after a tens, hundredths, or thousandths place or further to the right of the decimal just add a zero in the required areas.

Then add each place with the appropriately aligned number to get a result for each number.

In this case the decimals will add together like this 

The answer is .

To solve for  we must get all of the numbers on the other side of the equation of .

To do this in a problem where  is being multiplied by a coefficient, we must divide both sides of the equation by the coefficient.

In this case the number is  so we divide each side of the equation by  to make it look like this 

Then we must divide the decimals by each other to find the answer.

To divide decimals we line the decimals up like this 

Then ignoring all of the decimal places we divide the top number by the bottom number to get 

Then we must apply the decimals.

The number of decimal places in the denominator will be subtracted from the number of decimal places in the numerator to get the number of decimal places we must change our answer.

If the number is positive we move the decimal that number of places to the left of our number.

If the number is negative we move the decimal that number of places to the right of our number.

In this case it would be negative so we move the decimal  place to the right of  to get .

The answer is  .

To solve , add  to both sides.

To solve , we need to isolate . That means we need to add  to both sides.

To solve , you can either plug it into your calculator or realize that . Therefore, we are looking for half of five, which is .

Mathematically, that means: