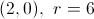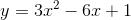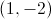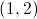All High School Math Resources
Example Questions
Example Question #5 : How To Find The Diameter Of A Sphere
What is the diameter of a sphere with a volume of 
The volume of a sphere is determined by the following equation:
Example Question #1 : How To Find The Radius Of A Sphere
Find the radius of a sphere whose surface area is 
Not enough information to solve
We know that the surface area of the spere is 
Rearrange and solve for 
Example Question #1 : How To Find The Radius Of A Sphere
What is the radius of a sphere that has a surface area of 
The standard equation to find the area of a sphere is 


To find the answer, substitute the given surface area into this equation and solve for the radius:
Example Question #3 : How To Find The Radius Of A Sphere
Given that the volume of a sphere is 
The standard equation to find the volume of a sphere is



Substitute the given volume into this equation and solve for the radius:
Example Question #4 : How To Find The Radius Of A Sphere
What is the radius of a sphere with a volume of 
Example Question #1 : Circles
What is the center and radius of the circle indicated by the equation?
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 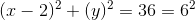


Example Question #1 : Pre Calculus
What is the shape of the graph indicated by the equation?
Hyperbola
Ellipse
Circle
Parabola
Ellipse
An ellipse has an equation that can be written in the format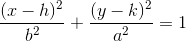

Example Question #2 : Pre Calculus
A conic section is represented by the following equation:
What type of conic section does this equation represent?
Ellipse
Parabola
Hyperbola
Circle
Hyperbola
The simplest way to know what kind of conic section an equation represents is by checking the coefficients in front of each variable. The equation must be in general form while you do this check. Luckily, this equation is already in general form, so it's easy to see. The general equation for a conic section is the following:
Assuming the term 
- If A equals C, the equation is a circle.
- If A and C have the same sign (but are not equal to each other), the equation is an ellipse.
- If either A or C equals 0, the equation is a parabola.
- If A and C are different signs (i.e. one is negative and one is positive), the equation is a hyperbola.
Example Question #2 : Pre Calculus
A conic section is represented by the following equation:
Which of the following best describes this equation?
vertical ellipse with center 
horizontal hyperbola with center of 

vertical parabola with vertex 
horizontal hyperbola with center 

vertical hyperbola with center 

horizontal hyperbola with center of 

First, we need to make sure the conic section equation is in a form we recognize. Luckily, this equation is already in standard form:
The first step is to determine the type of conic section this equation represents. Because there are two squared variables (

In a hyperbola, the squared term with a positive coefficient represents the direction in which the hyperbola opens. In other words, if the 

The center is always found at 

That leaves only the asymptotes. For a hyperbola, the slopes of the asymptotes can be found by dividing 



In this case, 



Example Question #3 : Pre Calculus
Find the vertex 
For any parabola of the form 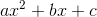
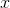
So here, we have
=
We plug this back into the original equation to find 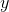
=
All High School Math Resources










![\sqrt[3]{27}=\sqrt[3]{r^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/154517/gif.latex)




















![\sqrt[3]{9}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/77809/gif.latex)
![\sqrt[3]{12 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/77815/gif.latex)


![r=\sqrt[3]{\frac{3V}{4\pi }}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/134330/gif.latex)
![r=\sqrt[3]{\frac{3V}{4\pi }}=\sqrt[3]{\frac{3\cdot 12\pi }{4\pi }}=\sqrt[3]{\frac{36\pi }{4\pi }}=\sqrt[3]{9 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/105139/gif.latex)










![\sqrt[3]{216}=\sqrt[3]{r^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/154557/gif.latex)